
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 的动圆恒与
的动圆恒与![]() 轴相切,
轴相切,![]() 为该圆的直径,设点
为该圆的直径,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的任意直线
的任意直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,
,![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,除
,除![]() 以外,直线
以外,直线![]() 与
与![]() 是否有其它公共点?说明理由.
是否有其它公共点?说明理由.
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC的所有棱长为1.M是底面△ABC内部一个动点(包括边界),且M到三个侧面PAB,PBC,PAC的距离h1,h2,h3成单调递增的等差数列,记PM与AB,BC,AC所成的角分别为α,β,γ,则下列正确的是( )
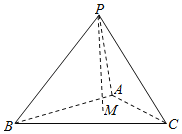
A.α=βB.β=γC.α<βD.β<γ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一动圆P与定圆![]() 外切,且与直线
外切,且与直线![]() 相切,记动点P的轨迹为曲线E.
相切,记动点P的轨迹为曲线E.
(1)求曲线E的方程;
(2)过点![]() 作直线l与曲线E交于不同的两点B、C,设BC中点为Q,问:曲线E上是否存在一点A,使得
作直线l与曲线E交于不同的两点B、C,设BC中点为Q,问:曲线E上是否存在一点A,使得![]() 恒成立?如果存在,求出点A的坐标;如果不存在,说明理由.
恒成立?如果存在,求出点A的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,
,![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三名乒乓球手进行单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得3分,负者得0分,在每一场比赛中,甲胜乙的概率为![]() ,丙胜甲的概率为
,丙胜甲的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为
,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)设在该次对抗比赛中,丙得分为![]() ,求
,求![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com