
(1)在区间[-2,6]上画出函数f(x)的图象;
(2)设集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞),试判断集合A和B之间的关系,并给出证明;
(3)当k>2时,证明在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
(1)解:
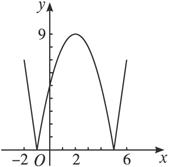
(2)解:方程f(x)=5的解分别是2-![]() ,0,4和2+
,0,4和2+![]() ,由于f(x)在(-∞,-1)和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此A=(-∞,2-
,由于f(x)在(-∞,-1)和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此A=(-∞,2-![]() )∪[0,4]∪[2+
)∪[0,4]∪[2+![]() ,+∞).
,+∞).
由于2+![]() <6,2-
<6,2-![]() >-2,
>-2,
∴B![]() A.
A.
(3)证法一:当x∈[-1,5]时,f(x)=-x2+4x+5,
g(x)=k(x+3)-(-x2+4x+5)
=x2+(k-4)x+(3k-5)
=(x-![]() )2-
)2-![]() ,
,
∵k>2,∴![]() <1.
<1.
又-1≤x≤5,
①当-1≤![]() <1,即2<k≤6时,取x=
<1,即2<k≤6时,取x=![]() ,g(x)min=-
,g(x)min=-![]() =-
=-![]() [(k-10)2-64].
[(k-10)2-64].
∵16≤(k-10)2<64,∴(k-10)2-64<0.则g(x)min>0.
②当![]() <-1,即k>6时,取x=-1,g(x)min=2k>0.
<-1,即k>6时,取x=-1,g(x)min=2k>0.
由①②,可知当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.
证法二:当x∈[-1,5]时,f(x)=-x2+4x+5.
由 得x2+(k-4)x+(3k-5)=0.
得x2+(k-4)x+(3k-5)=0.
令Δ=(k-4)2-4(3k-5)=0,解得k=2或k=18.
在区间[-1,5]上,当k=2时,y=2(x+3)的图象与函数f(x)的图象只交于一点(1,8);当k=18时,y=18(x+3)的图象与函数f(x)的图象没有交点.
由于直线y=k(x+3)过点(-3,0),当k>2时,直线y=k(x+3)是由直线y=2(x+3)绕点(-3,0)逆时针方向旋转得到的.因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 2e |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 15 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:徐州模拟 题型:解答题
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com