
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,M,N分别是
,M,N分别是![]() ,
,![]() 的中点,且
的中点,且![]() .
.

(1)求![]() 的长度;
的长度;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() ,
,![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的最大值和最小值.
的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
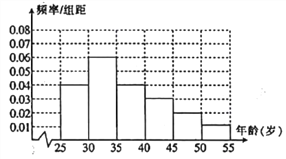
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
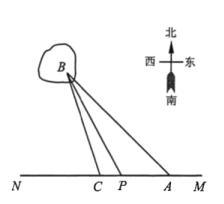
【题目】如图,某沿海地区计划铺设一条电缆联通A,B两地,A地位于东西方向的直线MN上的陆地处,B地位于海上一个灯塔处,在A地用测角器测得![]() ,在A地正西方向4km的点C处,用测角器测得
,在A地正西方向4km的点C处,用测角器测得![]() .拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设
.拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设![]() ,
,![]() ,铺设电缆的总费用为
,铺设电缆的总费用为![]() 万元.
万元.
(1)求函数![]() 的解析式;
的解析式;
(2)试问点P选在何处时,铺设的总费用最少,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数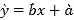 ,回归直线方程
,回归直线方程![]() ,
,
其中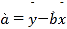 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
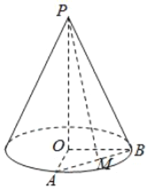
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,半径为
,半径为![]() .
.
(1)设圆锥的母线长为![]() ,求圆锥的体积;
,求圆锥的体积;
(2)设![]() ,
,![]() 、
、![]() 是底面半径,且
是底面半径,且![]() ,
,![]() 为线段
为线段![]() 的中点,如图.求异面直线
的中点,如图.求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有![]() 名四年级学生,将全体四年级学生随机按
名四年级学生,将全体四年级学生随机按![]() 编号,并且按编号顺序平均分成
编号,并且按编号顺序平均分成![]() 组.现要从中抽取
组.现要从中抽取![]() 名学生,各组内抽取的编号按依次增加
名学生,各组内抽取的编号按依次增加![]() 进行系统抽样.
进行系统抽样.
(1)若抽出的一个号码为![]() ,据此写出所有被抽出学生的号码;
,据此写出所有被抽出学生的号码;
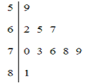
(2)分别统计这![]() 名学生的数学成绩,获得成绩数据的茎叶图如图所示,求该样本的方差.
名学生的数学成绩,获得成绩数据的茎叶图如图所示,求该样本的方差.
(注:![]() ,方差
,方差![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com