练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一个口袋内有4个不同的红球,6个不同的白球.
    (1)从中任取4个球,红球个数不少于白球个数的取法有多少种?
    (2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7的取法

    （1）115（2）186

    解析试题分析：解:(1)分三类:第一类有4个红球,则有种取法; 第二类有3个红球,则有种取法; 第三类有2个红球,则有种取法;各根据加法原理共有1+24+90=115种不同的取法.
    (2)若总分不少于7,则可以取4红1白,或3红2白,或2红3白,共3类,取法总数为
    种不同的取法.
    考点：计数原理的运用
    点评：解决的关键是利用分步乘法计数原理和分类加法计数原理来求解，属于基础题。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    为了解学生身高情况，某校以10%的比例对全校700名学生按性
    别进行分层抽样调查，测得身高情况的统计图如下：

    （1）估计该校男生的人数；
    （2）估计该校学生身高在170～185㎝之间的概率；
    （3）从样本中身高在165～180㎝之间的女生中任选2人，求至少有1人身高在170～180㎝之间的概率；

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知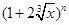的展开式中，某一项的系数是它前一项系数的2倍，而又等于它后一项系数的
    （Ⅰ）求展开后所有项的系数之和及所有项的二项式系数之和；
    （Ⅱ）求展开式中的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    已知二项式(N*)展开式中，前三项的二项式系数和是，求：
    (Ⅰ)的值；
    (Ⅱ)展开式中的常数项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设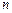是给定的正整数，有序数组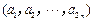同时满足下列条件：
    ① 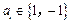,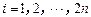； ②对任意的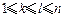,都有．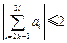
    （1）记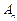为满足“对任意的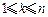，都有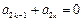”的有序数组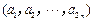的个数，求；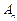
    （2）记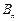为满足“存在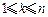，使得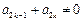”的有序数组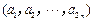的个数，求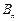

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）已知二项式(N*)展开式中，前三项的二项式系数和是，求：（Ⅰ）的值；（Ⅱ）展开式中的常数项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （满分12分）从1，3，5，7，9中任取三个数字，从2，4，6，8中任取两个数字，可以组成多少：（列出式子并用数字给出最后答案）
    （1）无重复数字的五位数；
    （2）万位、百位和个位数字是奇数的无重复数字的五位数；
    （3）千位和十位数字只能是奇数的无重复数字的五位数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知的展开式的二项式系数之和比(a＋b)2n的展开式的系数之和小240，求n的展开式中系数最大的项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    若；
    求：（1）；
    （2）；   
    （3）；

    查看答案和解析>>

    同步练习册答案