
 ,
,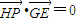 (G为动点,P是HP和GF的交点).
(G为动点,P是HP和GF的交点). (O为EF的中点).
(O为EF的中点).
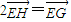 ,
,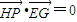 ,|PG|=|PE|,而|PF|+|PE|=|PG|=2a.由此能求出点P的轨迹方程.
,|PG|=|PE|,而|PF|+|PE|=|PG|=2a.由此能求出点P的轨迹方程.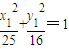 ,
,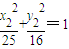 .由此入手能够证明|OC|<
.由此入手能够证明|OC|< .
. ,
,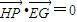 ,
,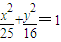 .…(4分)
.…(4分)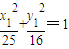 ,
,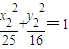 .
.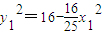 ,
, .
.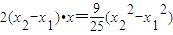 .
.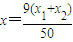 .
.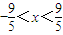 ,即|OC|<
,即|OC|< .…(13分)
.…(13分)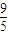 .解题时要认真审题,恰当地建立平面直角坐标系,灵活运用圆锥曲线的性质,合理地进行等价转化.
.解题时要认真审题,恰当地建立平面直角坐标系,灵活运用圆锥曲线的性质,合理地进行等价转化. 

科目:高中数学 来源: 题型:
 (2004•朝阳区一模)如图,已知PA垂直于正方形ABCD所在的平面,E、F分别为AB、PD的中点,过AE、AF的平面交PC于点H,二面角P-CD-B为45°,PA=a.
(2004•朝阳区一模)如图,已知PA垂直于正方形ABCD所在的平面,E、F分别为AB、PD的中点,过AE、AF的平面交PC于点H,二面角P-CD-B为45°,PA=a.查看答案和解析>>
科目:高中数学 来源: 题型:
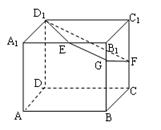
如图,已知正方体![]() 的棱长为2,E、F分别是
的棱长为2,E、F分别是![]() 、
、![]() 的中点,过
的中点,过![]() 、E、F作平面
、E、F作平面![]() 交
交![]() 于G..
于G..
(Ⅰ)求证:![]() ∥
∥![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面![]() 所截得的几何体
所截得的几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
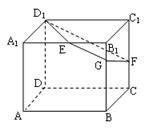
如图,已知正方体![]() 的棱长为2,E、F分别是
的棱长为2,E、F分别是![]() 、
、![]() 的中点,过
的中点,过![]() 、E、F作平面
、E、F作平面![]() 交
交![]() 于G..
于G..
(Ⅰ)求证:![]() ∥
∥![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面![]() 所截得的几何体
所截得的几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2011届广东省汕头市高三四校联考数学理卷 题型:解答题
.(本小题满分14分)
如图,已知正方体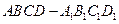 的棱长为2,E、F分别是
的棱长为2,E、F分别是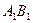 、
、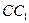 的中点,过
的中点,过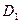 、E、F作平面
、E、F作平面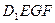 交
交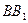 于G..
于G..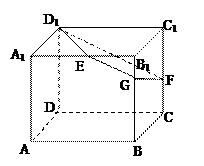
(Ⅰ)求证: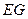 ∥
∥ ;
;
(Ⅱ)求二面角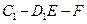 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面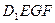
 所截得的几何体
所截得的几何体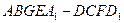 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕头市高三四校联考数学理卷 题型:解答题
.(本小题满分14分)
如图,已知正方体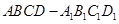 的棱长为2,E、F分别是
的棱长为2,E、F分别是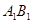 、
、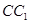 的中点,过
的中点,过 、E、F作平面
、E、F作平面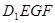 交
交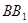 于G..
于G..

(Ⅰ)求证: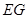 ∥
∥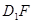 ;
;
(Ⅱ)求二面角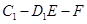 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面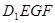 所截得的几何体
所截得的几何体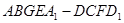 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com