
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\frac{{\sqrt{5}}}{2},+∞})$ | C. | $({1,\frac{5}{4}})$ | D. | $({\frac{5}{4},+∞})$ |
分析 由于双曲线的一条渐近线方程为:y=$\frac{b}{a}$x,及点(2,1)在“右”区域内,得出 $\frac{b}{a}$>$\frac{1}{2}$,从而得出双曲线离心率e的取值范围.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程为:y=$\frac{b}{a}$x,
∵点(2,1)在“右”区域内,
∴$\frac{b}{a}$×2>1,即$\frac{b}{a}$$>\frac{1}{2}$,
∴e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$>$\frac{\sqrt{5}}{2}$,
又e>1,
则双曲线离心率e的取值范围是($\frac{\sqrt{5}}{2}$,+∞).
故选:B.
点评 本小题主要考查双曲线的简单性质、不等式(组)与平面区域、不等式的性质等基础知识,考查运算求解能力与转化思想.属于基础题.


科目:高中数学 来源: 题型:选择题
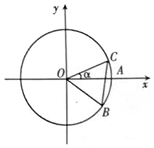 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{9}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com