公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为___________.
（参考数据：
）
科目：高中数学 来源：2017届宁夏高三上第二次月考文数试卷（解析版） 题型：解答题
已知函数
.
（1）若函数
在
上至少有一个零点，求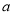
的取值范围；
（2）若函数在
上的最大值为3，求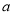的值.
查看答案和解析>>
科目：高中数学 来源：2016届浙江绍兴柯桥区高三二模文数试卷（解析版） 题型：解答题
如图，
、
是抛物线
上的两个点, 过点
、
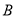引抛物线的两条弦
.
（1）求实数
的值；
（2）若直线
与
的斜率是互为相反数, 且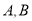
两点在直线
的两侧.
①直线的斜率是否为定值？若是求出该定值，若不是, 说明理由；
②求四边形
面积的取值范围.
查看答案和解析>>
科目：高中数学 来源：2016届浙江绍兴柯桥区高三二模文数试卷（解析版） 题型：选择题
已知
,则“
”是“
”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．即不充分又不必要条件
查看答案和解析>>
科目：高中数学 来源：2016届高三（亮剑·快乐考生）三轮冲刺猜题（三）文数试卷（解析版） 题型：解答题
中石化集团获得了某地深海油田区块的开采权，集团在该地区随机初步勘探了部分儿口井，取得了地质资料.进入全面勘探时期后，集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高，如果新设计的井位与原有井位重合或接近，便利用旧井的地质资料，不必打这口新井，以节约勘探费用．勘探初期数据资料见如表：
（Ⅰ）1～6号旧井位置线性分布，借助前5组数据求得回归直线方程为
，求
，并估计
的预报值；
（Ⅱ）现准备勘探新井
，若通过1、3、5、7号井计算出的
的值（精确到0.01）相比于（Ⅰ）中
的值之差不超过10%，则使用位置最接近的已有旧井
，否则在新位置打开，请判断可否使用旧井？
（参考公式和计算结果：
）
（Ⅲ）设出油量与勘探深度的比值
不低于20的勘探并称为优质井，那么在原有井号1～6的出油量不低于50L的井中任意勘探3口井，求恰好2口是优质井的概率.
查看答案和解析>>
科目：高中数学 来源：2016届高三（亮剑·快乐考生）三轮冲刺猜题（三）文数试卷（解析版） 题型：选择题
如图，
是边长为1的正方体，
是高为1的正四棱锥，若点
，
，
，
，
在同一个球面上，则该球的表面积为（ ）
A．
B．
C. 
D．
查看答案和解析>>
科目：高中数学 来源：2016-2017学年江苏扬州中学高二上开学考试数学卷（解析版） 题型：填空题
定义：区间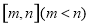
的长度为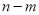
，已知函数
的定义域为
值域为
则区间
长度的最大值与最小值的差为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（
，
是虚数单位），则
（ ）
C．1 D．1或2
的图像向左平移
个单位，再向上平移1个单位，所得图像的函数解析式为 .