
ΓΨΧβΡΩΓΩ”–œ¬Ν–ΥΒΖ®ΘΚ
ΔΌ‘Ύ≤–≤νΆΦ÷–Θ§≤–≤νΒψ±»ΫœΨυ‘»ΒΊ¬δ‘ΎΥ°ΤΫΒΡ¥χΉ¥«χ”ρΡΎΘ§ΥΒΟς―Γ”ΟΒΡΡΘ–Ά±»ΫœΚœ ΘΜ
ΔΎ”ΟœύΙΊ÷Η ΐR2ά¥ΩΧΜ≠ΜΊΙιΒΡ–ßΙϊΘ§R2÷Β‘Ϋ¥σΘ§ΥΒΟςΡΘ–ΆΒΡΡβΚœ–ßΙϊ‘ΫΚΟΘΜ
Δέ±»ΫœΝΫΗωΡΘ–ΆΒΡΡβΚœ–ßΙϊΘ§Ω…“‘±»Ϋœ≤–≤νΤΫΖΫΚΆΒΡ¥σ–ΓΘ§≤–≤νΤΫΖΫΚΆ‘Ϋ–ΓΒΡΡΘ–ΆΘ§ΡβΚœ–ßΙϊ‘ΫΚΟΘ°
Δή‘Ύ―–ΨΩΤχΈ¬ΚΆ»»≤ηœζ έ±≠ ΐΒΡΙΊœΒ ±Θ§»τ«σΒΟœύΙΊ÷Η ΐR2Γ÷0.85Θ§‘ρ±μΟςΤχΈ¬Ϋβ ΆΝΥ15ΘΞΒΡ»»≤ηœζ έ±≠ ΐ±δΜ·.
Τδ÷–’ΐ»ΖΟϋΧβΒΡΗω ΐ «(ΓΓΓΓ)
A. 1 B. 2 C. 3 D. 4
ΓΨ¥πΑΗΓΩC
ΓΨΫβΈωΓΩΕ‘”ΎΔΌ‘Ύ≤–≤νΆΦ÷–Θ§≤–≤νΒψ±»ΫœΨυ‘»ΒΊ¬δ‘ΎΥ°ΤΫΒΡ¥χΉ¥«χ”ρΡΎΘ§ΥΒΟς―Γ”ΟΒΡΡΘ–Ά±»ΫœΚœ Θ§’ΐ»Ζ
Ε‘”ΎΔΎ”ΟœύΙΊ÷Η ΐR2ά¥ΩΧΜ≠ΜΊΙιΒΡ–ßΙϊΘ§R2÷Β‘Ϋ¥σΘ§ΥΒΟςΡΘ–ΆΒΡΡβΚœ–ßΙϊ‘ΫΚΟΘ§’ΐ»Ζ
Ε‘”ΎΔέ±»ΫœΝΫΗωΡΘ–ΆΒΡΡβΚœ–ßΙϊΘ§Ω…“‘±»Ϋœ≤–≤νΤΫΖΫΚΆΒΡ¥σ–ΓΘ§≤–≤νΤΫΖΫΚΆ‘Ϋ–ΓΒΡΡΘ–ΆΘ§ΡβΚœ–ßΙϊ‘ΫΚΟΘ§’ΐ»Ζ
Ε‘”ΎΔή‘Ύ―–ΨΩΤχΈ¬ΚΆ»»≤ηœζ έ±≠ ΐΒΡΙΊœΒ ±Θ§»τ«σΒΟœύΙΊ÷Η ΐR2Γ÷0.85Θ§‘ρ±μΟςΤχΈ¬Ϋβ ΆΝΥ15ΘΞΒΡ»»≤ηœζ έ±≠ ΐ±δΜ·Θ§¥μΈσΘ§”ΠΗΟ «ΤχΈ¬Ϋβ ΆΝΥ85ΘΞΒΡ»»≤ηœζ έ±≠ ΐ±δΜ·
Ι ―Γ![]()


 Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΚ”Ρœ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ Ά§≤ΫΝΖœΑΈςΡœ ΠΖΕ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑΈςΡœ ΠΖΕ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
![]()
Θ®1Θ©»τ![]() «“Κ· ΐ
«“Κ· ΐ![]() ΒΡ÷Β”ρΈΣ
ΒΡ÷Β”ρΈΣ![]() ,«σ
,«σ![]() ΒΡ±μ¥ο Ϋ;
ΒΡ±μ¥ο Ϋ;
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬, Β±![]() ±,
±, ![]() «ΒΞΒςΚ· ΐ, «σ Β ΐkΒΡ»Γ÷ΒΖΕΈß;
«ΒΞΒςΚ· ΐ, «σ Β ΐkΒΡ»Γ÷ΒΖΕΈß;
Θ®3Θ©…η![]() ,
, ![]()
![]() «“
«“![]() ΈΣ≈ΦΚ· ΐ, ≈–Εœ
ΈΣ≈ΦΚ· ΐ, ≈–Εœ![]() ΘΪ
ΘΪ![]() ΡήΖώ¥σ”ΎΝψ?«κΥΒΟςάμ”….
ΡήΖώ¥σ”ΎΝψ?«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©Έ ΧβΖΔœ÷
»γœ¬ΆΦΘ§ΓςACBΚΆΓςDCEΨυΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψAΓΔDΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ§Ν§Ϋ”BEΓΘ
ΧνΩ’ΘΚΔΌΓœAEBΒΡΕ» ΐΈΣ____________ΘΜ
ΔΎœΏΕΈADΓΔBE÷°ΦδΒΡ ΐΝΩΙΊœΒ «_________ΓΘ

Θ®2Θ©ΆΊ’ΙΧΫΨΩ
»γœ¬ΆΦΘ§ΓςACBΚΆΓςDCEΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœACB=ΓœDCE=900, ΒψAΓΔDΓΔE‘ΎΆ§“Μ÷±œΏ…œΘ§CMΈΣΓςDCE÷–DE±Ώ…œΒΡΗΏΘ§Ν§Ϋ”BEΓΘ«κ≈–ΕœΓœAEBΒΡΕ» ΐΦΑœΏΕΈCMΓΔAEΓΔBE÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΓΘ

Θ®3Θ©ΫβΨωΈ Χβ
»γœ¬ΆΦΘ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§CD=![]() ΓΘ»τΒψP¬ζΉψPD=1,«“ΓœBPD=900Θ§«κ÷±Ϋ”–¥≥ωΒψAΒΫBPΒΡΨύάκΓΘ
ΓΘ»τΒψP¬ζΉψPD=1,«“ΓœBPD=900Θ§«κ÷±Ϋ”–¥≥ωΒψAΒΫBPΒΡΨύάκΓΘ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() Θ§
Θ§ ![]() ΒΡ÷–ΒψΘ°ΫΪ
ΒΡ÷–ΒψΘ°ΫΪ![]() ―Ί
―Ί![]() ’έΤπΒΫ
’έΤπΒΫ![]() ΒΡΈΜ÷ΟΘ§ Ι
ΒΡΈΜ÷ΟΘ§ Ι![]() Θ§»γΆΦ2Θ§Ν§Ϋα
Θ§»γΆΦ2Θ§Ν§Ϋα![]() Θ§
Θ§ ![]() Θ°
Θ°
Θ®ΔώΘ©«σ÷ΛΘΚΤΫΟφ![]()
![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©»τ![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§«σ÷±œΏ
÷–ΒψΘ§«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘΜ
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘΜ
Θ®ΔσΘ©œΏΕΈ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψ
…œ «Ζώ¥φ‘Ύ“ΜΒψ![]() Θ§ ΙΕΰΟφΫ«
Θ§ ΙΕΰΟφΫ«![]() ΒΡ”ύœ“÷ΒΈΣ
ΒΡ”ύœ“÷ΒΈΣ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕ![]() ÷–Θ§ΥΡ±Ώ–Έ
÷–Θ§ΥΡ±Ώ–Έ![]() ΈΣΝβ–ΈΘ§
ΈΣΝβ–ΈΘ§ ![]() Θ§
Θ§ ![]() ΒΉΟφ
ΒΉΟφ![]() Θ§
Θ§ ![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œ“ΜΕ·ΒψΘ°
…œ“ΜΕ·ΒψΘ°
Θ®ΔώΘ©«σ÷ΛΘΚ ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©»τ![]() Θ§
Θ§ ![]() Ζ÷±πΈΣœΏΕΈ
Ζ÷±πΈΣœΏΕΈ![]() Θ§
Θ§ ![]() ΒΡ÷–ΒψΘ§«σ÷ΛΘΚ
ΒΡ÷–ΒψΘ§«σ÷ΛΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔσΘ©÷±œΏ![]() …œ «Ζώ¥φ‘ΎΒψ
…œ «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟΤΫΟφ
Θ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an}Θ§anΓί0Θ§a1=0Θ§an+12+an+1©¹1=an2Θ®nΓ NΘ©Θ°Φ«Sn=a1+a2+Γ≠+an Θ° Tn= ![]() +
+ ![]() +Γ≠+
+Γ≠+ ![]() Θ°«σ÷ΛΘΚΒ±nΓ N* ±
Θ°«σ÷ΛΘΚΒ±nΓ N* ±
Θ®1Θ©0ΓήanΘΦan+1ΘΦ1ΘΜ
Θ®2Θ©SnΘΨn©¹2ΘΜ
Θ®3Θ©TnΘΦ3Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΤΫΟφABCDΓΆΤΫΟφADEFΘ§Τδ÷–ABCDΈΣΨΊ–ΈΘ§ADEFΈΣΧί–ΈΘ§AFΓΈDEΘ§AFΓΆFEΘ§AF=AD=2DE=2Θ§‘ρ“λΟφ÷±œΏEF”κBCΥυ≥…Ϋ«¥σ–ΓΈΣ Θ° 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥφΜζ≥ι»ΓΡ≥ΗΏ÷–ΦΉΓΔ““ΝΫΗωΑύΗς10ΟϊΆ§―ßΘ§≤βΝΩΥϊΟ«ΒΡ…μΗΏ(ΒΞΈΜΘΚcm)Θ§ΜώΒΟ…μΗΏ ΐΨίΒΡΨΞ“ΕΆΦ»γΆΦΥυ ΨΘ°

(1)ΦΉΑύΚΆ““ΑύΆ§―ß…μΗΏΒΡ÷–ΈΜ ΐΗς «Εύ…ΌΘΩ≤ΔΦΤΥψΦΉΑύ―υ±ΨΒΡΖΫ≤νΘ°
(2)œ÷¥”““Αύ’β10ΟϊΆ§―ß÷–ΥφΜζ≥ι»Γ2Οϊ…μΗΏ≤ΜΒΆ”Ύ173 cmΒΡΆ§―ßΘ§«σ…μΗΏΈΣ176 cmΒΡΆ§―ß±Μ≥ι÷–ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏlΒΡ≤Έ ΐΖΫ≥ΧΈΣ 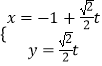 Θ®tΈΣ≤Έ ΐΘ©Θ§«ζœΏCΒΡΦΪΉχ±ξΖΫ≥Χ «Π―=
Θ®tΈΣ≤Έ ΐΘ©Θ§«ζœΏCΒΡΦΪΉχ±ξΖΫ≥Χ «Π―= ![]() Θ§“‘ΦΪΒψΈΣ‘≠ΒψΘ§ΦΪ÷αΈΣx÷α’ΐΖΫœρΫ®ΝΔ÷±Ϋ«Ήχ±ξœΒΘ§ΒψMΘ®©¹1Θ§0Θ©Θ§÷±œΏl”κ«ζœΏCΫΜ”ΎAΓΔBΝΫΒψΘ°
Θ§“‘ΦΪΒψΈΣ‘≠ΒψΘ§ΦΪ÷αΈΣx÷α’ΐΖΫœρΫ®ΝΔ÷±Ϋ«Ήχ±ξœΒΘ§ΒψMΘ®©¹1Θ§0Θ©Θ§÷±œΏl”κ«ζœΏCΫΜ”ΎAΓΔBΝΫΒψΘ°
Θ®ΔώΘ©–¥≥ω÷±œΏlΒΡΦΪΉχ±ξΖΫ≥Χ”κ«ζœΏCΒΡΤ’Ά®ΖΫ≥ΧΘΜ
Θ®ΔρΘ©«σœΏΕΈMAΓΔMB≥ΛΕ»÷°ΜΐMAMBΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com