
【题目】已知圆![]() :
:![]() 的圆心为
的圆心为![]() ,圆
,圆![]() :
:![]() 的圆心为
的圆心为![]() ,一动圆与圆
,一动圆与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是直线
是直线![]() 上任意点,直线
上任意点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,试探求
,试探求![]() ,
,![]() ,
,![]() 的关系,并给出证明.
的关系,并给出证明.
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=|2x+2|+|x﹣a|的最小值为2.

(1)求实数a的值,并作出y=f(x)的图象;
(2)当m>0,n>0,且m+n=2![]() 时,m2+n2≥f(x)恒成立,求实数x的取值范围.
时,m2+n2≥f(x)恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5B.21元C.21.5元D.22元
查看答案和解析>>
科目:高中数学 来源: 题型:
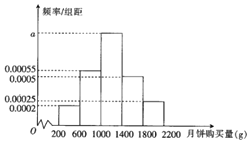
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房产中介统计了深圳市某高档小区从2018年12月至2019年11月当月在售二手房均价(单位:万元/平方米)的散点图,如下图所示,图中月份代码1至12分别对应2018年12月至2019年11月的相应月份.
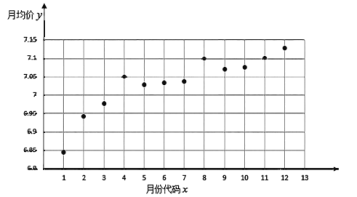
根据散点图选择![]() 和
和![]() 两个模型进行拟合,根据数据处理得到两个回归方程分别为
两个模型进行拟合,根据数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.0148557 | 0.0048781 |
总偏差平方和 | 0.069193 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2020年5月份购买深圳市福田区![]() 平方米的二手房(欲购房为其家庭首套房).若该小区所有住房的房产证均已满3年,请你利用(1)中拟合效果更好的模型解决以下问题:
平方米的二手房(欲购房为其家庭首套房).若该小区所有住房的房产证均已满3年,请你利用(1)中拟合效果更好的模型解决以下问题:
(i)估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.01万元/平方米)
(ii)若该购房者拟用不超过760万元的资金购买该小区一套二手房,试估算其可购买的最大面积(精确到1平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按照房屋的计税价格进行征收.(计税价格=房款)
征收方式见下表:
购买首套房面积 |
|
|
|
契税(买方缴纳)的税率 |
|
|
|
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关指数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为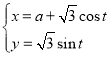 (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(异于极点),若
上(异于极点),若![]() 四点依次在同一条直线
四点依次在同一条直线![]() 上,且
上,且![]() 成等比数列,求
成等比数列,求![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若项数为![]() 的单调增数列
的单调增数列![]() 满足:①
满足:①![]() ;②对任意
;②对任意![]() ,存在
,存在![]()
![]() 使得
使得![]() ;则称数列
;则称数列![]() 具有性质
具有性质![]() .
.
(1)分别判断数列1,3,4,7和1,2,3,5是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若数列![]() 具有性质
具有性质![]() ,且
,且![]() .
.
(i)证明数列![]() 的项数
的项数![]() ;
;
(ii)求数列![]() 中所有项的和的最小值.
中所有项的和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com