
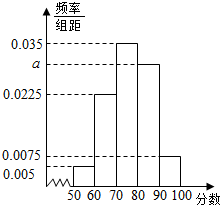
 某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.分析 (1)根据频率分布直方图中的数据高度与频率的关系,可得可以求解.
(2)依题意,X的可能取值是1,2,3. 利用概率知识得出P(X=1),P(X=2),P(X=3)=P(A),即可得出分布列,数学期望的值.
解答 解:(1)根据频率分布直方图中的数据,可得:
a=$\frac{1-(0.005+0.0075+0.0225+0.0035)×10}{10}$=0.1-0.07=0.03,
所以 a=0.03.
(2)学生成绩在[50,60)内的共有40×0.05=2人,在[60,70)内的共有40×0.225=9人,
成绩在[50,70)内的学生共有11人.
依题意,X的可能取值是1,2,3.
P(X=1)=$\frac{{{C}_{2}^{2}C}_{9}^{1}}{{C}_{11}^{3}}$=$\frac{3}{55}$;
P(X=2)=$\frac{{{C}_{2}^{1}C}_{9}^{2}}{{C}_{11}^{3}}$=$\frac{24}{55}$;
P(X=3)=P(A)=$\frac{28}{55}$,P(A)=$\frac{{C}_{9}^{3}}{{C}_{11}^{3}}$=$\frac{28}{55}$
所以X的分布列为
| X | 1 | 2 | 3 |
| P | $\frac{3}{55}$ | $\frac{24}{55}$ | $\frac{28}{55}$ |
点评 本题综合考察了离散型的概率问题,考察了学生的阅读分析问题的能力,分类讨论的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
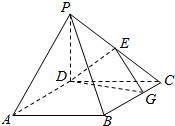 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,-1) | B. | (0,1) | C. | (0,$\sqrt{2014×2015}$) | D. | (0,$\sqrt{\frac{2014}{2015}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?$x>0,\;\;x+\frac{1}{x}$<2 | B. | ?$x≤0,\;\;x+\frac{1}{x}$<2 | C. | ?$x≤0,\;\;x+\frac{1}{x}$<2 | D. | ?$x>0,\;\;x+\frac{1}{x}$<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com