
 ��ͼ����������y2=4x�ϵĵ�A��1��2��������l��x����ֱ��x=-4�ֱ���D��B������P��������y2=4x�ϵ�һ�㣬��E���߶�AP�ϣ�����
��ͼ����������y2=4x�ϵĵ�A��1��2��������l��x����ֱ��x=-4�ֱ���D��B������P��������y2=4x�ϵ�һ�㣬��E���߶�AP�ϣ�����| AE |
| EP |
| BF |
| FP |
| BD |
| DA |
| BD |
| 3 |
| 2 |
| DA |
| PD |
| ||||||
1+
|
| 2 |
| 5 |
| PB |
| 3 |
| 5 |
| PA |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| y0-m |
| x0+3 |
 �⣺��1������AB��y=x+1��D��-1��0����
�⣺��1������AB��y=x+1��D��-1��0����| BD |
| DA |
| BD |
| 3 |
| 2 |
| DA |
| PD |
| ||||||
1+
|
| 2 |
| 5 |
| PB |
| 3 |
| 5 |
| PA |
| PQ |
| PD |
| 2 |
| 5 |
| PA |
| 3 |
| 5 |
| PE |
| 2 |
| 5 |
| PF |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 4 |
| PD |
| 1 |
| 3 |
|
|
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| y0-m |
| x0+3 |
| -2y0 |
| x0+1 |
| -(x0+3) |
| x0+1 |
| 1 |
| 2 |
| 1 |
| 2 |
[
|
| (4t2+20t-9)(t+2)2 |
| t2 |
| 3 |
| 4 |
11
| ||
| 12 |


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
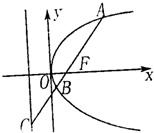 ��ͼ����������y2=2px��p��0���Ľ���F��ֱ��l���������ڵ�A��B���������ڵ�C����|BC|=2|BF|����|AF|=3����������ߵķ���Ϊ
��ͼ����������y2=2px��p��0���Ľ���F��ֱ��l���������ڵ�A��B���������ڵ�C����|BC|=2|BF|����|AF|=3����������ߵķ���Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 78����ͼ����������y2=4x�Ľ���F��ֱ�߽���������Բ��x-1��2+y2=1��A��B��C��D�ĵ㣬��|AB|•|CD|=
78����ͼ����������y2=4x�Ľ���F��ֱ�߽���������Բ��x-1��2+y2=1��A��B��C��D�ĵ㣬��|AB|•|CD|=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����������y2=2px��p��0���Ľ���F��ֱ��l���������ڵ�A��B��|AF|��|BF|�����������ڵ�C����|BC|=2|BF|����|AF|=2����������ߵķ���Ϊ
��ͼ����������y2=2px��p��0���Ľ���F��ֱ��l���������ڵ�A��B��|AF|��|BF|�����������ڵ�C����|BC|=2|BF|����|AF|=2����������ߵķ���Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����������y2=2px��p��0���Ľ���F����б��Ϊ60���ֱ��l����������A��B���㣬��|AF|=3����������߷���Ϊ��������
��ͼ����������y2=2px��p��0���Ľ���F����б��Ϊ60���ֱ��l����������A��B���㣬��|AF|=3����������߷���Ϊ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����������y2=4x�����ֱ�����ν���������Բ��x-1��2+y2=1��A��B��C��D����
��ͼ����������y2=4x�����ֱ�����ν���������Բ��x-1��2+y2=1��A��B��C��D����| AB |
| CD |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com