
【题目】袋中有红、白球各一个,每次任取一个,有放回地摸三次,求基本事件的个数n,写出所有基本事件的全集I,并计算下列事件的概率:
(1)三次颜色恰有两次同色;
(2)三次颜色全相同;
(3)三次摸到的红球多于白球.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
利用列举法,列举出所有的可能事件.
(1)根据上述分析,根据古典概型概率计算公式,计算出三次颜色恰有两次同色的概率.
(2)根据上述分析,根据古典概型概率计算公式,计算出三次颜色全相同的概率.
(3)根据上述分析,根据古典概型概率计算公式,计算出三次摸到的红球多于白球的概率
基本事件个数![]() ,全集
,全集![]() {(红,红,红),(红,红,白),(红,白,红),(红,白,白),(白,红,红),(白,红,白),(白,白,红),(白,白,白)}.
{(红,红,红),(红,红,白),(红,白,红),(红,白,白),(白,红,红),(白,红,白),(白,白,红),(白,白,白)}.
(1)记事件A为“三次颜色恰有两次同色”.
∵A中含有基本事件个数为![]() ,
,
![]() .
.
(2)记事件B为“三次颜色全相同”.
∵B中含有基本事件个数为![]() ,
,
![]() .
.
(3)记事件C为“三次摸到的红球多于白球”.
∵C中含有基本事件个数为![]() ,
,
![]()


科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,求n≥m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足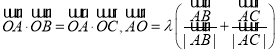 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩合格的概率分别为![]() ,
,![]() ,
,![]() ,若对这三名短跑运动员的100米跑的成绩进行一次检测.
,若对这三名短跑运动员的100米跑的成绩进行一次检测.
(1)求三人都合格的概率;
(2)求三人都不合格的概率;
(3)求出现几人合格的概率最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆系方程![]() :
: ![]() (
(![]() ,
, ![]() ),
), ![]() 是椭圆
是椭圆![]() 的焦点,
的焦点, ![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() 且与椭圆
且与椭圆![]() 相切的直线
相切的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,求证:
,求证: ![]() 的面积为定值,并求出这个定值.
的面积为定值,并求出这个定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出,任意三角形的外心、重心、垂心位于同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标为
A. (-4,0) B. (-3,-1) C. (-5,0) D. (-4,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若将频率视为概率,现从全市高二学生中随机查看5名学生的期中考试语文成绩,记成绩优秀(不低于80分)的学生人数为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:

(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com