设a,b,c都是正数,求证:
(1)(a+b+c)

≥9;
(2)(a+b+c)

≥

.
证明 (1)∵a,b,c都是正数,
∴a+b+c≥3

,

+

+

≥3

.
∴(a+b+c)

≥9,
当且仅当a=b=c时,等号成立.
(2)∵(a+b)+(b+c)+(c+a)
≥3

,
又

≥

,
∴(a+b+c)

≥

,
当且仅当a=b=c时,等号成立.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知:

, 求证:

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)定义:对于函数
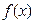
,
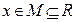
.若
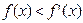
对定义域内的
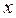
恒成立,则称函数
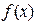
为
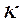
函数.(1)请举出一个定义域为
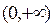
的
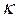
函数,并说明理由;(2)对于定义域为
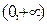
的
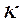
函数
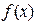
,求证:对于定义域内的任意正数
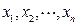
,均有
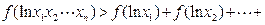
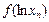
;
(3)对于值域
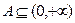
的
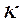
函数
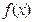
,求证:
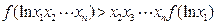
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知f(x)=
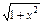
,a≠b,
求证:|f(a)-f(b)|<|a-b|.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知
i,
m、
n是正整数,且1<
i≤
m<
n.
(1)证明:
niA
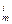
<
miA
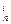

(2)证明: (1+
m)
n>(1+
n)
m
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(1)解不等式
≥3;
(2)a,b∈R
+,2c>a+b,求证
c-<a<c+.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
用数学归纳法证明1+
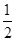
+
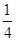
+…+
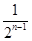
>
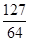
(n∈N
*)成立,其初始值至少应取( )
查看答案和解析>>

 ≥9;
≥9; ≥
≥ .
. 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案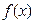 ,
,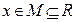 .若
.若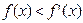 对定义域内的
对定义域内的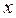 恒成立,则称函数
恒成立,则称函数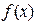 为
为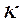 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为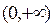 的
的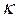 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为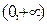 的
的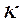 函数
函数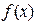 ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数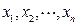 ,均有
,均有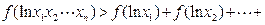
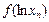 ;
;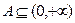 的
的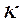 函数
函数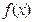 ,求证:
,求证: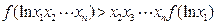 .
.