
【题目】设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示. 
(1)求A,ω,φ的值;
(2)设θ为锐角,且f(θ)=﹣ ![]() ,求f(θ﹣
,求f(θ﹣ ![]() )的值.
)的值.
【答案】
(1)解:由图象,得 ![]() ,
,
∵最小正周期 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
由 ![]() ,得
,得 ![]() ,k∈Z,
,k∈Z,
∴ ![]() ,k∈Z,
,k∈Z,
∵0<φ<π,
∴ ![]() .
.
(2)解:由 ![]() ,得
,得 ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)由图象可得A,最小正周期T,利用周期公式可求ω,由 ![]() ,得
,得 ![]() ,k∈Z,结合范围0<φ<π,可求φ的值(2)由已知可求
,k∈Z,结合范围0<φ<π,可求φ的值(2)由已知可求 ![]() ,由
,由 ![]() ,结合
,结合 ![]() ,可得范围
,可得范围 ![]() ,利用同角三角函数基本关系式可求cos(2θ+
,利用同角三角函数基本关系式可求cos(2θ+ ![]() )的值,利用两角差的正弦函数公式即可计算得解.
)的值,利用两角差的正弦函数公式即可计算得解.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (a>b>0)的图象是曲线C.
(a>b>0)的图象是曲线C. 
(1)在如图的坐标系中分别做出曲线C的示意图,并分别标出曲线C与x轴的左、右交点A1 , A2 .
(2)设P是曲线C上位于第一象限的任意一点,过A2作A2R⊥A1P于R,设A2R与曲线C交于Q,求直线PQ斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
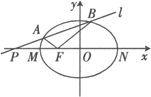
【题目】如图,设![]() 是椭圆
是椭圆![]() 的左焦点,点
的左焦点,点![]() 是
是![]() 轴上的一点,点
轴上的一点,点![]() 为椭圆的左、右顶点,已知
为椭圆的左、右顶点,已知![]() ,且
,且![]()
(1)求椭圆的标准方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,试判定直线
两点,试判定直线![]() 的斜率之和
的斜率之和![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn= ![]() ,数列{cn}的前n项和为Tn=
,数列{cn}的前n项和为Tn= ![]() .求n.
.求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=﹣2101 , 且当2≤n≤100时,an+2a102﹣n=3×2n恒成立,则数列{an}的前100项和S100= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区. 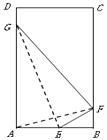
(1)请确定入口F的选址范围;
(2)设商业区的面积为S1 , 绿化区的面积为S2 , 商业区的环境舒适度指数为 ![]() ,则入口F如何选址可使得该商业区的环境舒适度指数最大?
,则入口F如何选址可使得该商业区的环境舒适度指数最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
![]() 存在每个面都是直角三角形的四面体;
存在每个面都是直角三角形的四面体;
![]() 若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;
若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;
![]() 棱台的侧棱延长后交于一点;
棱台的侧棱延长后交于一点;
![]() 用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
其中正确命题的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com