
【题目】给出下列四个命题: ①若a<b,则a2<b2;
②若a≥b>﹣1,则 ![]() ≥
≥ ![]() ;
;
③若正整数m和n满足m<n,则 ![]() ≤
≤ ![]() ;
;
④若x>0,且x≠1,则lnx+ ![]() ≥2.
≥2.
其中所有真命题的序号是
科目:高中数学 来源: 题型:
【题目】若函数![]() ,
,![]() ,则函数
,则函数![]() 的图像经过怎样的变换可以得到函数
的图像经过怎样的变换可以得到函数![]() 的图像
的图像
①先向左平移![]() 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的![]() 倍,纵坐标保持不变.
倍,纵坐标保持不变.
②先向左平移![]() 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的![]() 倍,纵坐标保持不变.
倍,纵坐标保持不变.
③将横坐标缩短到原来的![]() 倍,再向左平移
倍,再向左平移![]() 个单位,纵坐标保持不变.
个单位,纵坐标保持不变.
④将横坐标缩短到原来的![]() 倍,再向左平移
倍,再向左平移![]() 个单位,纵坐标保持不变.
个单位,纵坐标保持不变.
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同而颜色互不相同的小球若干个, 其中标号为0的小球1个, 标号为1的小球1个, 标号为2的小球2个, 从袋子中不放回地随机抽取2个小球, 记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1) 记事件![]() 表示“
表示“![]() ”, 求事件
”, 求事件![]() 的概率;
的概率;
(2) 在区间![]() 内任取2个实数
内任取2个实数![]() , 记
, 记![]() 的最大值为
的最大值为![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线方程为
的准线方程为![]() ,点
,点![]() 为坐标原点,不过点
为坐标原点,不过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)如果直线![]() 过点
过点![]() ,求证:
,求证:![]() ;
;
(2)如果![]() ,证明:直线
,证明:直线![]() 必过一定点,并求出该定点.
必过一定点,并求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
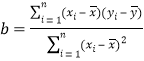 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1)(x∈R).
=(cosx,1)(x∈R).
(1)求f(x)的周期和单调递减区间;
(2)在△ABC 中,角A、B、C的对边分别为a,b,c,f(A)=﹣1,a= ![]() ,
, ![]()
![]() =3,求边长b和c的值(b>c).
=3,求边长b和c的值(b>c).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com