
(本小题14分)在数列 中,
中, =0,且对任意k
=0,且对任意k ,
, 成等差数列,其公差为2k. (Ⅰ)证明
成等差数列,其公差为2k. (Ⅰ)证明 成等比数列;
成等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)记 . 证明: 当
. 证明: 当 为偶数时, 有
为偶数时, 有 .
.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源:2012-2013学年江西省高三4月月考数学文理合卷试卷(解析版) 题型:解答题
理科(本小题14分)已知函数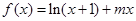 ,当
,当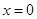 时,函数
时,函数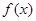 取得极大值.
取得极大值.
(Ⅰ)求实数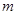 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数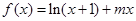 在区间
在区间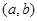 内导数都存在,且
内导数都存在,且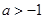 ,则存在
,则存在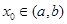 ,使得
,使得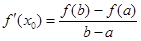 .试用这个结论证明:若
.试用这个结论证明:若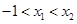 ,函数
,函数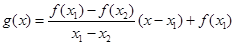 ,则对任意
,则对任意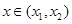 ,都有
,都有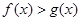 ;(Ⅲ)已知正数
;(Ⅲ)已知正数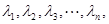 满足
满足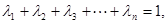 求证:当
求证:当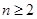 ,
,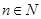 时,对任意大于
时,对任意大于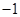 ,且互不相等的实数
,且互不相等的实数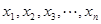 ,都有
,都有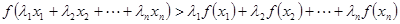
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下学期第二次月考数学试卷(解析版) 题型:解答题
(本小题14分)在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为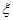 (
(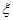 所有取值为0,1,2,3...,10)分别为
所有取值为0,1,2,3...,10)分别为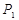 、
、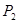 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
|
|
0 |
0 |
0 |
0 |
0.04 |
|
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
① 若1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
② ②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高一上学期期末考试数学试卷 题型:解答题
(本小题14分)
某市的一家报刊摊点,从报社买进《晚报》的价格是每份0.20元,卖出价是每份0.30元,卖不掉的报纸可以以每份0.05元价格退回报社.在一个月(以30天计)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题14分) (以下二题选做其一)
(1)甲乙两运动员进行射击训练,已知他们击中的环数都稳定在![]() 环内,且每次射击成绩互不影响,射击环数的频率分布条形图如下图所示,若将频率视为概率,回答下列问题.
环内,且每次射击成绩互不影响,射击环数的频率分布条形图如下图所示,若将频率视为概率,回答下列问题.
(Ⅰ)求甲运动员在一次射击中击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(Ⅱ)求甲运动员在![]() 次射击中至少有
次射击中至少有![]() 次击中
次击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(Ⅲ)若甲、乙两运动员各射击![]() 次,
次,![]() 表示这
表示这![]() 次射击中击中
次射击中击中![]() 环以上(含
环以上(含![]() 环)的次数,求
环)的次数,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
将一颗骰子先后抛掷2次,观察向上的点数,求:
(Ⅰ)两数之和为5的概率;
(Ⅱ)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆![]() =15的内部的概率.
=15的内部的概率.
21(本小题14分)已知![]() 的展开式的系数和大992。 求
的展开式的系数和大992。 求![]() 的展开式中;(1)二项式系数最大的项;(2)系数的绝对值最大的项。
的展开式中;(1)二项式系数最大的项;(2)系数的绝对值最大的项。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com