
分析 (1)将m=$\frac{1}{2}$代入得到f(x)的解析式,根据解析式要有意义,列出不等式,求解即可得到f(x)的定义域;
(2)将f(x)在(-∞,-1]上恒取正值,等价为f(x)>0在(-∞,-1]上恒成立,转化为f(x)min>0,利用f(x)的单调性即可求出f(x)的最小值,从而列出不等式,求解即可得到m的取值范围.
解答 解:(1)当m=$\frac{1}{2}$时,f(x)=lg[($\frac{1}{2}$)x-2x],
∴($\frac{1}{2}$)x-2x>0,即2-x>2x,
∴-x>x,即x<0,
∴函数f(x)的定义域为{x|x<0};
(2)设x2<0,x1<0,且x2>x1,
∴x2-x1>0,
令g(x)=mx-2x,
∴g(x2)-g(x1)=mx2-2x2-mx1+2x1=mx2-mx1+2x1-2x2,
∵0<m<1,x1<x2<0,
∴mx2-mx1<0,2x1-2x2<0,
∴g(x2)-g(x1)<0,即g(x2)<g(x1),
∴lg(g(x2))<lg(g(x1)),
∴lg(g(x2))-lg(g(x1))<0,
∴f(x2)<f(x1),
∴f(x)在(-∞,0)上是减函数,
∴f(x)在(-∞,-1]上是单调递减函数,
∴f(x)在(-∞,-1]上的最小值为f(-1)=lg(m-1-2-1),
∵f(x)在(-∞,-1]上恒取正值,即f(x)>0在(-∞,-1]上恒成立,
∴f(x)min>0,
∴f(-1)=lg(m-1-2-1)>0,即m-1-2-1>1,
∴$\frac{1}{m}$>1+$\frac{1}{2}$=$\frac{3}{2}$,
∵0<m<1,
∴0<m<$\frac{2}{3}$,
故m的取值范围为0<m<$\frac{2}{3}$.
点评 本题考查了函数定义域的求解,函数单调性的判断及其证明,函数恒成立问题的求解.对于求函数的定义域即求使得解析式有意义的x的取值集合.函数恒成立问题的,一般选用参变量分离法、最值法、数形结合法进行求解.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4π}{3}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
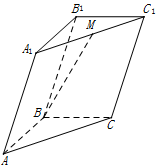
| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证:
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com