
| C | 3 5 |
| 1 |
| 2 |
| C | 4 5 |
| 1 |
| 2 |
| C | 5 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 64 |
| 3 |
| 32 |
| 15 |
| 64 |
| 5 |
| 16 |
| 15 |
| 64 |
| 3 |
| 32 |
| 1 |
| 64 |

| 1 |
| 2 |


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 16 |
| 3 |
| 8 |
| 2k2+1 |
| 36 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年江西上高二中、新余钢铁中学高三年级全真模拟数学(理科)试题 题型:解答题
上海世博会上有一种舞台灯,外形是正六棱柱,在其每个侧面(编号分别是①②③④⑤⑥)上安装5只颜色各异的灯,每只灯正常发光的概率是0.5,若一侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用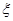 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个侧面面上恰有2个侧面需要更换的概率。
(3)写出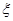 的分布列,并求出
的分布列,并求出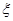 的数学期望。
的数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com