
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,存在
时,存在![]() 使不等式
使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:
试题解析:(I)借助存在型不等式成立的条件建立不等式;(II)先建立不等式,再运用导数知识求解:
解:(Ⅰ)当![]() 时,
时,![]() ,
,
所以![]() ,由
,由![]() 知
知![]() ,
,
则函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则当![]() 时,
时,![]() ,
,
故存在![]() 使不等式
使不等式![]() 成立,
成立,
只需![]() 即可.
即可.
(Ⅱ)在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方等价于对任意
的下方等价于对任意![]() ,
,![]() ,
,
即![]() 恒成立,
恒成立,
设![]() ,
,![]() .
.
则![]()
当![]() 时,
时,![]() ,
,![]() .
.
①若![]() ,即
,即![]() ,有
,有![]() ,
,
则函数![]() 在区间
在区间![]() 为减函数,
为减函数,
则对任意![]() ,
,![]() ,
,
只需![]() ,即当
,即当![]() 时,
时,![]() 恒成立.
恒成立.
②若![]() ,即
,即![]() 时,
时,
令![]() ,
,
得![]() .
.
则函数![]() 在区间
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
③若![]() ,即当
,即当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
综上,当![]() 时,
时,![]() 在区间
在区间![]() 恒成立,
恒成立,
即当![]() 时,在区间
时,在区间![]() 上函数
上函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方.
的下方.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】设命题p:f(x)=2/(x-m)在区间(1,+∞)上是减函数;;命题q:2x-1+2m>0对任意x∈R恒成立.若(![]() p)∧q为真,求实数m的取值范围。
p)∧q为真,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
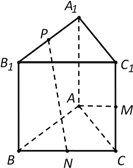
【题目】如图,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,第(1)问 4 分,第(2)问 8 分)
某闯关游戏规则是:先后掷两枚骰子,将此实验重复![]() 轮,第
轮,第![]() 轮的点数分别记为
轮的点数分别记为![]() ,如果点数满足
,如果点数满足![]() ,则认为第
,则认为第![]() 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束。
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束。
求第一轮闯关成功的概率;
如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com