
如图,在四棱锥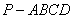 中,
中,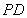
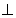 底面
底面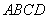 ,且底面
,且底面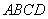 为正方形,
为正方形,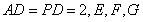 分别为
分别为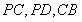 的中点.
的中点.
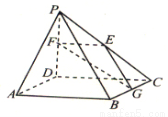
(1)求证: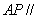 平面
平面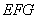 ;
;
(2)求平面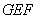 和平面
和平面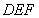 的夹角.
的夹角.
(1)详见解析;(2) .
.
【解析】
试题分析:(1)证明直线 平面
平面 ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,还可以利用面面平行的性质,本题由于
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,还可以利用面面平行的性质,本题由于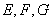 分别为
分别为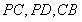 的中点,可得
的中点,可得 ,
,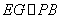 ,容易证明平面
,容易证明平面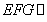 平面
平面 ,可得直线
,可得直线 平面
平面 ;本题还可用向量法,由于
;本题还可用向量法,由于
 底面
底面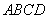 ,且底面
,且底面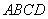 为正方形,可以
为正方形,可以 为原点,以
为原点,以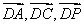 分别为
分别为 轴,建立空间坐标系,由题意写出各点的坐标,从而得
轴,建立空间坐标系,由题意写出各点的坐标,从而得 ,设平面
,设平面 的法向量为
的法向量为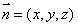 ,求出一个法向量,计算出
,求出一个法向量,计算出 ,即可;(2)求平面
,即可;(2)求平面 和平面
和平面 的夹角,可用向量法,由(1)解法二可知平面
的夹角,可用向量法,由(1)解法二可知平面 的法向量,由题意可知:
的法向量,由题意可知: 平面
平面 ,故向量
,故向量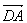 是平面
是平面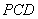 的一个法向量,利用夹角公式即可求出平面
的一个法向量,利用夹角公式即可求出平面 和平面
和平面 的夹角.
的夹角.
试题解析:(1)如图,以 为原点,以
为原点,以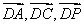 为方向向量
为方向向量
建立空间直角坐标系
则 .
.
 . 4分
. 4分
设平面 的法向量为
的法向量为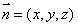
 即
即
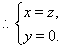 令
令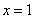 , 首发
, 首发
则 . 4分
. 4分

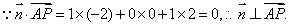
又 平面
平面 平面
平面 6分
6分
(2) 底面
底面 是正方形,
是正方形,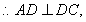 又
又 平面
平面
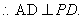 又
又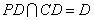 ,
, 平面
平面 。 8分
。 8分
 向量
向量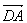 是平面
是平面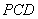 的一个法向量,
的一个法向量, 又由(1)知平面
又由(1)知平面 的法向量
的法向量 . 10分
. 10分

 二面角
二面角 的平面角为
的平面角为 . 12分
. 12分
考点:用空间向量求平面间的夹角;直线与平面平行的判定.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-3练习卷(解析版) 题型:解答题
如图所示,在直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上的点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与CD有怎样的位置关系?

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-3练习卷(解析版) 题型:填空题
如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,FG=2,则CF的长为________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-1练习卷(解析版) 题型:解答题
如图,在?ABCD中,设E和F分别是边BC和AD的中点,BF和DE分别交AC于P、Q两点.

求证:AP=PQ=QC.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-1练习卷(解析版) 题型:选择题
如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE等于( ).
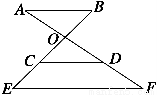
A.9 B.10
C.11 D.12
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试理科数学试卷(解析版) 题型:填空题
如图所示,在一个边长为1的正方形 内,曲线
内,曲线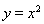 和曲线
和曲线 围成一个叶形图(阴影部分),向正方形
围成一个叶形图(阴影部分),向正方形 内随机投一点(该点落在正方形
内随机投一点(该点落在正方形 内任何一点是等可能的),则所投的点落在叶形图内部的概率是 .
内任何一点是等可能的),则所投的点落在叶形图内部的概率是 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试理科数学试卷(解析版) 题型:选择题
一个空间几何体的三视图如图所示,则该几何体的表面积为( )

A. 48 B. C.
C. D.80
D.80
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com