
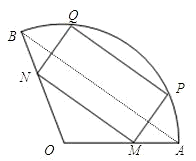
 如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?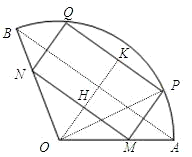 解:连接OP,设∠AOP=θ,则θ∈(0°,120°),
解:连接OP,设∠AOP=θ,则θ∈(0°,120°),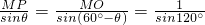
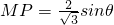 ①(5分)
①(5分)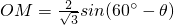 ,
, (10分)
(10分)
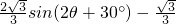 (13分)
(13分)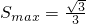 ,(15分)
,(15分) 的长是
的长是 的长的
的长的 时(或说成当∠AOP=30°时),
时(或说成当∠AOP=30°时), .(16分)
.(16分)

 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
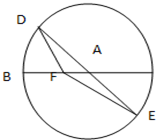 如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且
如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且| BF |
| FA |
| FD |
| FE |
A、-
| ||
B、-
| ||
C、-
| ||
| D、不确定 |
查看答案和解析>>
科目:高中数学 来源:陕西省模拟题 题型:解答题
 ,点P是半圆上的动点,以
,点P是半圆上的动点,以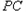 为边作等边三角形
为边作等边三角形 ,且点D与圆心分别在
,且点D与圆心分别在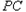 的两侧.
的两侧. ,试将四边形
,试将四边形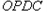 的面积
的面积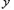 表示成
表示成 的函数;
的函数;  的面积的最大值.
的面积的最大值.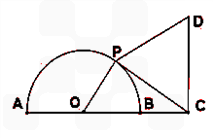
查看答案和解析>>
科目:高中数学 来源:陕西省模拟题 题型:解答题
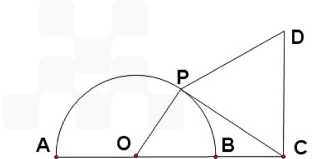
如图,已知 的半径是1,点在直径AB的延长线上, BC=1, 点P是
的半径是1,点在直径AB的延长线上, BC=1, 点P是 上半圆上的动点, 以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
上半圆上的动点, 以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
(Ⅰ) 若 ,试将四边形OPDC的面积y表示成θ的函数;
,试将四边形OPDC的面积y表示成θ的函数;
(Ⅱ) 求四边形OPDC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省武汉二中高一(下)期末数学试卷(解析版) 题型:选择题
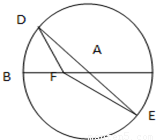 如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且
如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则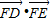 的值是( )
的值是( )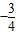

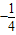
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省济宁市嘉祥一中高三(下)段考数学试卷(文科)(解析版) 题型:选择题
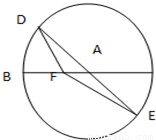 如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且
如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且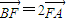 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则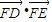 的值是( )
的值是( )

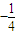
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com