
【题目】某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮。假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于( )。
【答案】![]()
【解析】
试题根据题意,记该选手恰好回答了4个问题就晋级下一轮为A,
若该选手恰好回答了4个问题就晋级下一轮,
必有第二个问题回答错误,第三、四个回答正确,第一个问题可对可错;
有相互独立事件的概率乘法公式,
可得P(A)=1×0.2×0.8×0.8=0.128,
故答案为0.128.
法二:根据题意,记该选手恰好回答了4个问题就晋级下一轮为A,
若该选手恰好回答了4个问题就晋级下一轮,
必有第二个问题回答错误,第三、四个回答正确,第一个问题可对可错,由此分两类,第一个答错与第一个答对;
有相互独立事件的概率乘法公式,
可得P(A)=0.8×0.2×0.8×0.8+0.2×0.2×0.8×0.8=0.2×0.8×0.8=0.128


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: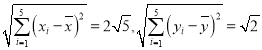
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: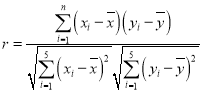 ,
,
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为![]() .
.
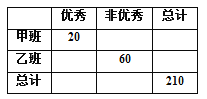
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附: 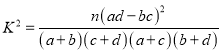
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省积极响应教育部号召实行新课程改革,为了调查某校高三学生的物理考试成绩是否达到![]() 级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
考试成绩达到 | 考试成绩未达到 | 总计 | |
男生 | 26 | 40 | |
女生 | 6 | ||
总计 | 70 |
(1)(ⅰ)将![]() 列联表补充完整;
列联表补充完整;
(ⅱ)据此列联表判断,能否有![]() 的把握认为“物理考试成绩是否达到级与性别有关”?
的把握认为“物理考试成绩是否达到级与性别有关”?
(2)将频率视作概率,从该校高三年级任意抽取3名学生的成绩,求物理考试成绩达到![]() 级的人数的分布列及期望.
级的人数的分布列及期望.
附: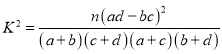
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为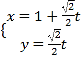 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求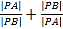 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校开设了射击选修课,规定向![]() 、
、![]() 两个靶进行射击:先向
两个靶进行射击:先向![]() 靶射击一次,命中得1分,没有命中得0分,向
靶射击一次,命中得1分,没有命中得0分,向![]() 靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向
靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,向
,向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
(1)求小明同学恰好命中一次的概率;
(2)求小明同学获得总分![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com