
【题目】如图,在底面是菱形的四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=60°,PA=AB=2,点E,F分别为BC,PD的中点,设直线PC与平面AEF交于点Q.
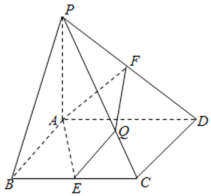
(1)已知平面PAB∩平面PCD=l,求证:AB∥l.
(2)求直线AQ与平面PCD所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证明AB∥平面PCD,然后利用直线与平面平行的性质定理证明AB∥l;
(2)以点A为原点,直线AE、AD、AP分别为轴建立空间直角坐标系,求出平面PCD的法向量和直线AQ的方向向量,然后利用空间向量的数量积求解直线AQ与平面PCD所成角的正弦值即可.
(1)证明:∵AB∥CD,AB![]() 平面PCD,CD平面PCD.
平面PCD,CD平面PCD.
∴AB∥平面PCD,
∵AB平面PAB,平面PAB∩平面PCD=l,
∴AB∥l;
(2)∵底面是菱形,E为BC的中点,且AB=2,
∴![]() ,
,
∴AE⊥AD,又PA⊥平面ABCD,则以点A为原点,直线AE、AD、AP分别为x、y、z轴建立如图所示空间直角坐标系,

则![]() ,
,
∴![]() ,
,![]() ,
,
设平面PCD的法向量为![]() ,有
,有![]() ,
,![]() ,得
,得![]() ,
,
设![]() ,则
,则![]() ,
,
再设![]() ,
,
则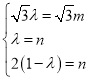 ,解之得
,解之得![]() ,∴
,∴![]() ,
,
设直线AQ与平面PCD所成角为α,
则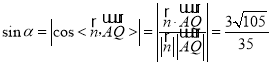 ,
,
∴直线AQ与平面PCD所成角的正弦值为![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴非负半轴为极轴建立极坐标系,已知直线
轴非负半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为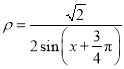 ,曲线
,曲线![]() 的参数方程为
的参数方程为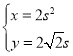 (
(![]() 为参数).
为参数).
(1)若直线![]() 平行于直线
平行于直线![]() ,且与曲线
,且与曲线![]() 只有一个公共点,求直线
只有一个公共点,求直线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种气垫船的最大航速是![]() 海里小时,船每小时使用的燃料费用和船速的平方成正比.若船速为
海里小时,船每小时使用的燃料费用和船速的平方成正比.若船速为![]() 海里小时,则船每小时的燃料费用为
海里小时,则船每小时的燃料费用为![]() 元,其余费用(不论船速为多少)都是每小时
元,其余费用(不论船速为多少)都是每小时![]() 元。甲乙两地相距
元。甲乙两地相距![]() 海里,船从甲地匀速航行到乙地.
海里,船从甲地匀速航行到乙地.
(1)试把船从甲地到乙地所需的总费用![]() ,表示为船速
,表示为船速![]() (海里小时)的函数,并指出函数的定义域;
(海里小时)的函数,并指出函数的定义域;
(2)当船速为每小时多少海里时,船从甲地到乙地所需的总费用最少?最少费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() ,圆
,圆![]() 的方程是
的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上任意一点
上任意一点![]() 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为大于40岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() 、
、![]() (
(![]() ),设函数
),设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 、
、![]() 、
、![]() 为长度的线段能否组成一个三角形,如果不一定,进一步求出
为长度的线段能否组成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能组成一个三角形;
的取值范围,使它们能组成一个三角形;
(3)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
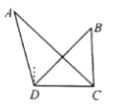
【题目】如图所示,为了测量A、B处岛屿的距离,小海在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶20海里至C处,观测B在C处的正北方向,A在C处的北偏西45°方向,则A、B两岛屿的距高为___________海里.
查看答案和解析>>
科目:高中数学 来源: 题型:
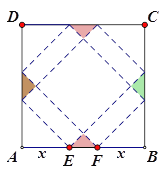
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得![]() 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
(1)若广告商要求包装盒侧面积S(cm![]() )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm![]() )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com