
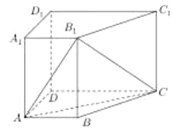
【题目】如图,在直四棱柱![]() 中,
中,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() :
:
(1)求证:![]() 平面
平面![]() ;
;
(2)现将与四棱柱![]() 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为![]() ,写出
,写出![]() 的解析式;(直接写出答案,不必说明理由)
的解析式;(直接写出答案,不必说明理由)
【答案】(1)详见解析:(2)4种不同的拼接方案,f(k)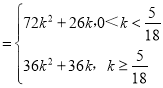
【解析】
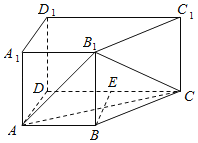
(1)取DC的中点E,连接BE,可证明四边形ABED是平行四边形,再利用勾股定理的逆定理可得BE⊥CD,即CD⊥AD,又侧棱AA1⊥底面ABCD,可得AA1⊥DC,利用线面垂直的判定定理即可证明.
(2)由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案,新四棱柱共有此4种不同方案.通过比较即可得出f(k).
(1)证明:取DC的中点E,连接BE,∵AB∥ED,AB=ED=3k,
∴四边形ABED是平行四边形,
∴BE∥AD,且BE=AD=4k,∴BE2+EC2=(4k)2+(3k)2=(5k)2=BC2,∴∠BEC=90°,∴BE⊥CD,
又∵BE∥AD,∴CD⊥AD.
∵侧棱AA1⊥底面ABCD,∴AA1⊥CD,
∵AA1∩AD=A,∴CD⊥平面ADD1A1.
(2)由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案新四棱柱共有此4种不同方案.
通过比较即可得出f(k)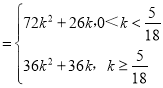 .
.


科目:高中数学 来源: 题型:
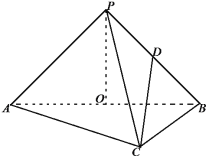
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 分别是
分别是![]() 的中点,
的中点,![]() ,连接
,连接![]() .
.
(1)若![]() ,并异面直线
,并异面直线![]() 与
与![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(2)若二面角![]() 的余弦值的大小为
的余弦值的大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,2),圆![]() ,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求点M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,若椭圆上的点与两个焦点构成的三角形中,面积最大为1.
,若椭圆上的点与两个焦点构成的三角形中,面积最大为1.
(1)求椭圆的标准方程;
(2)设直线![]() 与椭圆的交于
与椭圆的交于![]() 两点,
两点,![]() 为坐标原点,且
为坐标原点,且![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,D(0,2)为椭圆C短轴的一个端点,F为椭圆C的右焦点,线段DF的延长线与椭圆C相交于点E,且|DF|=3|EF|.
(1)求椭圆C的标准方程;
(2)设直线l与椭圆C相交于A,B两点,O为坐标原点,若直线OA与OB的斜率之积为-![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射手每次射击击中目标的概率是![]() ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.
(Ⅰ)假设这名射手射击![]() 次,求有
次,求有![]() 次连续击中目标,另外
次连续击中目标,另外![]() 次未击中目标的概率;
次未击中目标的概率;
(Ⅱ)假设这名射手射击![]() 次,记随机变量
次,记随机变量![]() 为射手击中目标的次数,求
为射手击中目标的次数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年的天猫“双11”交易金额又创新高,达到2684亿元,物流爆增.某机构为了了解网购者对收到快递的满意度进行调查,对某市5000名网购者发出满意度调查评分表,收集并随机抽取了200名网购者的调查评分(评分在70~100分之间),其频率分布直方图如图,评分在95分及以上确定为“非常满意”.
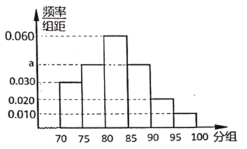
(1)求![]() 的值;
的值;
(2)以样本的频率作概率,试估计本次调查的网购者中“非常满意”的人数;
(3)按分层抽样的方法,从评分在90分及以上的网购者中抽取6人,再从这6人中随机地选取2人,求至少选到一个“非常满意”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com