
【题目】棱台![]() 的三视图与直观图如图所示.
的三视图与直观图如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(1)见解析.(2)![]() 在
在![]() 的中点.
的中点.
【解析】试题分析:(1)首先根据三视图特征可得![]() 平面
平面![]() ,
, ![]() 为正方形,所以
为正方形,所以![]() .再由
.再由![]() 即可得线面垂直从而得出面面垂直(2)直接建立空间坐标系写出各点坐标求出法向量,在根据向量的交角公式得出等式求出
即可得线面垂直从而得出面面垂直(2)直接建立空间坐标系写出各点坐标求出法向量,在根据向量的交角公式得出等式求出![]()
解析:(1)根据三视图可知![]() 平面
平面![]() ,
, ![]() 为正方形,
为正方形,
所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,
为坐标原点, ![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系,如图所示,
轴建立空间直角坐标系,如图所示,
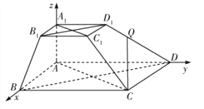
根据三视图可知![]() 为边长为2的正方形,
为边长为2的正方形, ![]() 为边长为1的正方形,
为边长为1的正方形,
![]() 平面
平面![]() ,且
,且![]() .
.
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
因为![]() 在
在![]() 上,所以可设
上,所以可设![]() .
.
因为![]() ,所以
,所以![]()
![]() .
.
所以![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
根据
令![]() ,可得
,可得![]() ,所以
,所以![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以
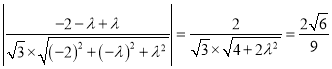 .
.
所以![]() ,即点
,即点![]() 在
在![]() 的中点位置.
的中点位置.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
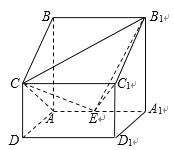
(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长度;
的长度;
(Ⅲ)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?(结论不要求证明)
?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
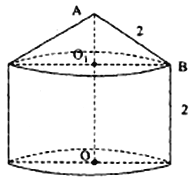
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某商场旅游鞋的日销售情况,现抽取部分顾客购鞋的尺码,将所得数据绘成如图所示频率分布直方图,已知图中从左到右前三组的频率之比为1:2:3,第二组的频数为10. 
(1)用频率估计概率,求尺码落在区间(37.5,43.5]概率约是多少?
(2)从尺码落在区间(37.5,39.5](43.5,45.5]顾客中任意选取两人,记在区间(43.5,45.5]的人数为X,求X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

(已知![]() ,
,  ).
).
(1)求出![]() 的值;
的值;
(2)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;(3)用
;(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个数据中任取2个,求抽取的2个数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个数据中任取2个,求抽取的2个数据中至少有1个是“好数据”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com