
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
【答案】D
【解析】
根据题意知,每次涂成红色的数字成等差数列,并且第n次染色时所染的最后一个数是n(2n-1),可以求出2019个数是在第45次染色的倒数第7个数,因此可求得结果.
第1此染色的数为1=1![]() ,共染色1个,
,共染色1个,
第2次染色的最后一个数为6=2![]() ,共染色3个,
,共染色3个,
第3次染色的最后一个数为15=3![]() ,共染色5个,
,共染色5个,
第4次染色的最后一个数为28=4![]() ,共染色7个,
,共染色7个,
第5次染色的最后一个数为45=5![]() ,共染色9个,
,共染色9个,
…
∴第n次染色的最后一个数为n![]() ,共染色2n-1个,
,共染色2n-1个,
经过n次染色后被染色的数共有1+3+5+…+(2n-1)=n2个,
而2019![]() ,
,
∴第2019个数是在第45次染色时被染色的,第45次染色的最后一个数为45![]() ,且相邻两个数相差2,
,且相邻两个数相差2,
∴2019=45![]() =3993.
=3993.
故选:D.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空数集A如果满足:①0A;②若对x∈A,有 ![]() ∈A,则称A是“互倒集”.给出以下数集: ①{x∈R|x2+ax+1=0}; ②{x|x2﹣4x+1<0};③{y|y=
∈A,则称A是“互倒集”.给出以下数集: ①{x∈R|x2+ax+1=0}; ②{x|x2﹣4x+1<0};③{y|y=  }.
}.
其中“互倒集”的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 满足:f(1)=1,f(﹣2)=4.
满足:f(1)=1,f(﹣2)=4.
(1)求a,b的值,并探究是否存在常数c,使得对函数f(x)在定义域内的任意x,都有f(x)+f(c﹣x)=4成立;
(2)当x∈[1,2]时,不等式f(x)≤ ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若 ![]() 且sinC=cosA (Ⅰ)求角A、B、C的大小;
且sinC=cosA (Ⅰ)求角A、B、C的大小;
(Ⅱ)函数f(x)=sin(2x+A)+cos(2x﹣ ![]() ),求函数f(x)单调递增区间,指出它相邻两对称轴间的距离.
),求函数f(x)单调递增区间,指出它相邻两对称轴间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
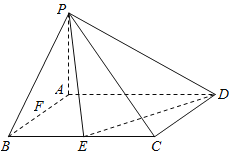
【题目】在四棱锥![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是线段BC,AB的中点.
,E,F是线段BC,AB的中点.
![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在线段PA上确定点G,使得
在线段PA上确定点G,使得![]() 平面PED,请说明理由.
平面PED,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2+ax﹣lnx(a∈R). (Ⅰ)当a=1时,求函数f(x)的极值;
x2+ax﹣lnx(a∈R). (Ⅰ)当a=1时,求函数f(x)的极值;
(Ⅱ)当a>1时,讨论函数f(x)的单调性;
(Ⅲ)若对任意a∈(3,4)及任意x1 , x2∈[1,2],恒有 ![]() m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下判断正确的是( )
A. 命题“负数的平方是正数”不是全称命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
C. “![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的必要不充分条件
”的必要不充分条件
D. “![]() ”是“函数
”是“函数![]() 是偶函数”的充要条件
是偶函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问250名不同性别的高中生在购买食物时是否看营养说明书,得到如下列联表:
女 | 男 | 总计 | |
读营养说明书 | 90 | 60 | 150 |
不读营养说明书 | 30 | 70 | 100 |
总计 | 120 | 130 | 250 |
从调查的结果分析,认为性别和读营养说明书的关系为( )
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
A. 95%以上认为无关 B. 90%~95%认为有关 C. 95%~99.9%认为有关 D. 99.9%以上认为有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com