
已知 .
.
当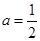 时,解不等式
时,解不等式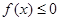 ;
;
(2)若 ,解关于
,解关于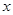 的不等式
的不等式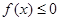 .
.
(1) ;(2)当
;(2)当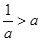 时,不等式的解集为
时,不等式的解集为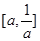 ;当
;当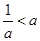 时,不等式的解集为
时,不等式的解集为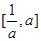 ;
;
当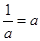 时,等式的解集为
时,等式的解集为 .
.
解析试题分析:(1)当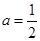 ,
,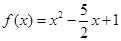 ,令
,令 ,则
,则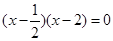 ,则由一元二次不等式与二次函数及一元二次方程三者之间的关系可知,不等式的解集为
,则由一元二次不等式与二次函数及一元二次方程三者之间的关系可知,不等式的解集为 ;(2)一元二次方程
;(2)一元二次方程 的两根为
的两根为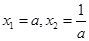 ,根据一元二次不等式与一元二次方程之间的关系可知,需对
,根据一元二次不等式与一元二次方程之间的关系可知,需对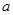 与
与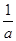 的大小关系分以下三种情况讨论:当
的大小关系分以下三种情况讨论:当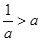 时,不等式的解集为
时,不等式的解集为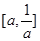 ;当
;当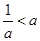 时,不等式的解集为
时,不等式的解集为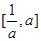 ;当
;当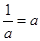 时,不等式的解集为
时,不等式的解集为 .
.
试题解析:(1)当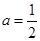 时,有不等式
时,有不等式 , 2分
, 2分
∴ ,∴不等式的解集为
,∴不等式的解集为 ; 4分
; 4分
(2)∵不等式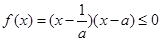 ,一元二次方程
,一元二次方程 ,两根为
,两根为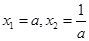 ,
,
∴当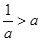 时,有
时,有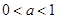 ,∴不等式的解集为
,∴不等式的解集为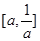 ; 7分
; 7分
当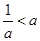 时,有
时,有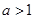 ,∴不等式的解集为
,∴不等式的解集为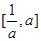 ; 10分
; 10分
当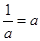 时,有
时,有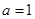 ,∴不等式的解集为
,∴不等式的解集为 . 12分
. 12分
考点:1.一元二次不等式、二次函数、一元二次方程三个二次之间的关系;2.分类讨论的数学思想.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com