Question

【题目】（附加题，本小题满分10分，该题计入总分）

已知函数，若在区间内有且仅有一个，使得成立，则称函数具有性质．

（1）若，判断是否具有性质，说明理由；

（2）若函数具有性质，试求实数的取值范围．

Answer 1

【答案】（Ⅰ）具有性质; （Ⅱ）或或

【解析】

试题（Ⅰ）具有性质．若存在，使得，解方程求出方程的根，即可证得；（Ⅱ）依题意，若函数具有性质，即方程在上有且只有一个实根．设，即在上有且只有一个零点．讨论的取值范围，结合零点存在定理，即可得到的范围．

试题解析：（Ⅰ）具有性质．

依题意，若存在 ，使，则 时有，即，，．由于 ，所以．又因为区间内有且仅有一个，使成立，所以具有性质5分

（Ⅱ）依题意，若函数具有性质，即方程在上有且只有一个实根．

设，即在上有且只有一个零点．

解法一：

（1）当时，即时，可得在上为增函数，

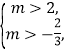只需解得交集得．

（2）当时，即时，若使函数在上有且只有一个零点，需考虑以下3种情况：

（ⅰ）时，在上有且只有一个零点，符合题意．

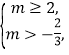（ⅱ）当即时，需解得交集得．

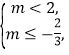（ⅲ）当时，即时，需解得交集得．

（3）当时，即时，可得在上为减函数

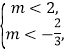只需解得交集得．

综上所述，若函数具有性质，实数的取值范围是或或14分

解法二：

依题意，

（1）由得，，解得或．

同时需要考虑以下三种情况：

（2）由解得．

（3）由解得不等式组无解．

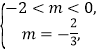（4）由解得解得．

综上所述，若函数具有性质，实数的取值范围是或

或14分．