
【题目】已知函数![]() 定义域为
定义域为![]() ,设
,设![]() .
.
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(2)求证:![]() ;
;
(3)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,并确定这样的
,并确定这样的![]() 的个数.
的个数.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.

(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中对几何学的研究比西方早一千多年.在该书中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;将底面为矩形,一侧棱垂直于底面的四棱锥称为阳马;将四个面均为直角三角形的四面体称为鳖臑.如图,在堑堵![]() 中,
中,![]() ,
,![]() ,鳖臑
,鳖臑![]() 的体积为2,则阳马
的体积为2,则阳马![]() 外接球表面积的最小值为__________.
外接球表面积的最小值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有4张奖券,奖券上分别印有200元、400元、600元和800元字样,抽到奖券可获得相应奖金.6位客户有放回的进行抽取,每人随机抽取一张奖券,求6位客户中购买产品的客户人均所得奖金不少于500元的概率.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从8名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?(用数字结尾)
(1)甲、乙两人必须跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒.
查看答案和解析>>
科目:高中数学 来源: 题型:
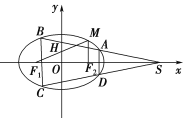
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为1.
的面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() 且使
且使![]() 轴,如图,问四边形
轴,如图,问四边形![]() 的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com