
【题目】椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,右顶点为B,且满足
,右顶点为B,且满足![]()
![]() Ⅰ
Ⅰ![]() 求椭圆的离心率e;
求椭圆的离心率e;
![]() Ⅱ
Ⅱ![]() 设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点
设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点![]() ,问是否存在过
,问是否存在过![]() 的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() ,直线
,直线 ![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数![]() ,使得对定义域
,使得对定义域![]() 内的任意
内的任意![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 在其定义域
在其定义域 ![]() 上是“
上是“![]() 利普希兹条件函数”.
利普希兹条件函数”.
(1)若函数![]() 是“
是“![]() 利普希兹条件函数”,求常数
利普希兹条件函数”,求常数![]() 的最小值;
的最小值;
(2)判断函数![]() 是否是“
是否是“![]() 利普希兹条件函数”,若是,请证明,若不是,请说明理由;
利普希兹条件函数”,若是,请证明,若不是,请说明理由;
(3)若![]() 是周期为2的“
是周期为2的“![]() 利普希兹条件函数”,证明:对任意的实数
利普希兹条件函数”,证明:对任意的实数![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关平面向量分解定理的四个命题:
(1)一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
(2)一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
(3)平面向量的基向量可能互相垂直;
(4)一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.
其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
(1)根据表,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
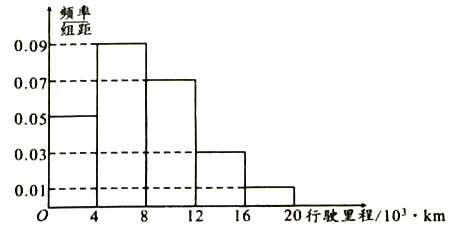
(2)图给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法从![]() 岁以上车主中抽取
岁以上车主中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送免费保养券,求这
人赠送免费保养券,求这![]() 人中至少有
人中至少有![]() 辆轿车的概率。
辆轿车的概率。
附:![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点P是圆M:
,动点P是圆M:![]() 上的任意一点,线段NP的垂直平分线和半径MP相交于点Q.
上的任意一点,线段NP的垂直平分线和半径MP相交于点Q.
![]() 求
求![]() 的值,并求动点Q的轨迹C的方程;
的值,并求动点Q的轨迹C的方程;
![]() 若圆
若圆![]() 的切线l与曲线C相交于A,B两点,求
的切线l与曲线C相交于A,B两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P在圆柱![]() 的底面圆
的底面圆![]() 上,AB为圆
上,AB为圆![]() 的直径,圆柱
的直径,圆柱![]() 的表面积为20π,
的表面积为20π,![]()
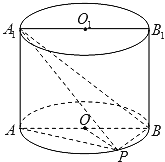
(1)求异面直线![]() 与AP所成角的大小(结果用反三角函数值表示);
与AP所成角的大小(结果用反三角函数值表示);
(2)求点A到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是椭圆![]() 上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com