
 如图,△ABC是等腰直角三角形∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE
如图,△ABC是等腰直角三角形∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE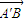 、
、 的坐标,利用垂直向量数量积为零建立方程组,解出
的坐标,利用垂直向量数量积为零建立方程组,解出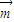 =(-,1,1)是平面A'BE的一个法向量;同理解出平面A'CD的一个法向量
=(-,1,1)是平面A'BE的一个法向量;同理解出平面A'CD的一个法向量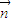 =(0,1,0).最后利用空间向量的夹角公式算出
=(0,1,0).最后利用空间向量的夹角公式算出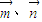 夹角的余弦值,结合图形即可得到四棱锥A'-BCDE体积取最大值时平面A′CD与平面A′BE夹角的余弦值.
夹角的余弦值,结合图形即可得到四棱锥A'-BCDE体积取最大值时平面A′CD与平面A′BE夹角的余弦值. BC,且F∥BC、GF=
BC,且F∥BC、GF= BC.
BC.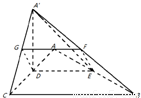
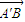 =(a,2a,-a),
=(a,2a,-a),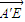 =(0,a,-a),
=(0,a,-a),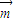 =(x,y,z),
=(x,y,z),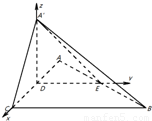
 得
得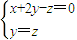
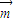 =(-,1,1),
=(-,1,1),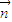 =(0,1,0)
=(0,1,0)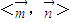 =
=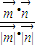 =
= =
=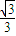
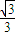
 ----(12分)
----(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
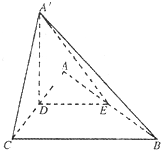 (2013•郑州一模)如图,△ABC是等腰直角三角形∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE
(2013•郑州一模)如图,△ABC是等腰直角三角形∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE查看答案和解析>>
科目:高中数学 来源: 题型:

| BD |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•郑州一模)如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE.
(2013•郑州一模)如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE.查看答案和解析>>
科目:高中数学 来源:2011年湖南省上学期高二学考模拟试题三 题型:解答题
如图,△ABC是等腰直角三角形, AC=BC=a,P是△ABC所在平面外一点,PA=PB=PC= a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.
a. (1)求证:平面PAB⊥平面ABC;(2)求PC与△ABC所在平面所成的角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com