已知抛物线y2=4x上两定点A、B分别在对称轴两侧,F为焦点,且|AF|=2,|BF|=5,在抛物线的AOB一段上求一点P,使S△ABP最大,并求面积最大值.
分析:先由题设条件知,|FA|=2,|FB|=5,可根据抛物线的定义求得点A、B的坐标;再由两点坐标已知,故由两点间距离公式求出两点的距离,由直线方程的两点式求出直线AB的方程;欲求△PAB的面积最大值可转化为求点P到直线AB的距离的最大值,设出点P的坐标,由点到直线的距离公式建立起点P到直线AB的距离的函数关系式,利用函数的知识求出最值即可.
解答: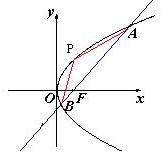
解:不妨设点A在第一象限,B点在第四象限.如图.
抛物线的焦点F(1,0),点A在第一象限,设A(x
1,y
1),y
1>0,
由|FA|=2得x
1+1=2,x
1=1,代入y
2=4x中得y
1=2,所以A(1,2),…(2分);
同理B(4,-4),…(4分)
由A(1,2),B(4,-4)得
|AB|==3…(6分)
直线AB的方程为
=,化简得2x+y-4=0.…(8分)
再设在抛物线AOB这段曲线上任一点P(x
0,y
0),且0≤x
0≤4,-4≤y
0≤2.
则点P到直线AB的距离d=
=
=
…(9分)
所以当y
0=-1时,d取最大值
,…(10分)
所以△PAB的面积最大值为S=
×3
×
=
…(11分)
此时P点坐标为(
,-1).…(12分).
点评:本小题主要考查抛物线的应用、直线与圆锥曲线的位置关系、两点间距离公式、点到直线的距离公式、直线方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

 解:不妨设点A在第一象限,B点在第四象限.如图.
解:不妨设点A在第一象限,B点在第四象限.如图.

 阅读快车系列答案
阅读快车系列答案 已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.
已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.