
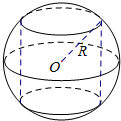
 如图所示,半径R=2的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于8π.
如图所示,半径R=2的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于8π. 科目:高中数学 来源: 题型:选择题
| A. | y=1+$\sqrt{x-1}$(x>1) | B. | y=1-$\sqrt{x-1}$(x>1) | C. | y=1+$\sqrt{x-1}$(x≥1) | D. | y=1-$\sqrt{x-1}$(x≥1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\underset{lim}{x→{x}_{0}}$f(x)和$\underset{lim}{x→{x}_{0}}$g(x)都不存在,则$\underset{lim}{x→{x}_{0}}$[f(x)+g(x)]不存在 | |
| B. | 若$\underset{lim}{x→{x}_{0}}$f(x)和$\underset{lim}{x→{x}_{0}}$g(x)都不存在,则$\underset{lim}{x→{x}_{0}}$[f(x)g(x)]不存在 | |
| C. | $\underset{lim}{x→{x}_{0}}$$\frac{f(x)}{g(x)}$存在,且$\underset{lim}{x→{x}_{0}}$[g(x)]=0,则$\underset{lim}{x→{x}_{0}}$f(x)=0 | |
| D. | 若$\underset{lim}{x→{x}_{0}}$|f(x)|=|A|,$\underset{lim}{x→{x}_{0}}$f(x)=A. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.求:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
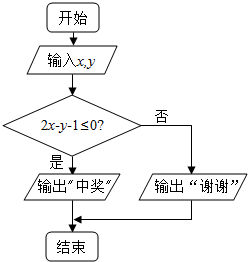 某单位抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,则该代表中奖的概率为( )
某单位抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,则该代表中奖的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com