
【题目】选修4-5:不等式选讲
已知函数![]() (其中
(其中![]() ).
).
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】试题分析:(1)方法一:分类讨论去掉绝对值,转化为一般的不等式,即可求解不等式的解集;
方法二:去掉绝对值,得到分段函数,画出函数的图象,结合图象即可求解不等式的解集.
(2)不等式![]() 即关于
即关于![]() 的不等式
的不等式![]() 恒成立,利用绝对值不等式,得
恒成立,利用绝对值不等式,得![]() ,进而求解实数
,进而求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)当![]() 时,函数
时,函数![]() ,
,
则不等式为![]() ,
,
①当![]() 时,原不等式为
时,原不等式为![]() ,解得:
,解得: ![]() ;
;
②当![]() 时,原不等式为
时,原不等式为![]() ,解得:
,解得: ![]() .此时不等式无解;
.此时不等式无解;
③当![]() 时,原不等式为
时,原不等式为![]() ,解得:
,解得: ![]() ,
,
原不等式的解集为![]() .
.
方法二:当![]() 时,函数
时,函数![]()
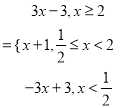 ,画出函数
,画出函数![]() 的图象,如图:
的图象,如图:
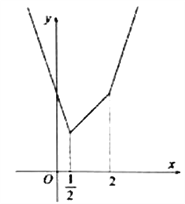
结合图象可得原不等式的解集为![]() .
.
(2)不等式![]() 即为
即为![]()
![]() ,
,
即关于![]() 的不等式
的不等式![]() 恒成立.
恒成立.
而![]()
![]()
![]()
![]() ,
,
所以![]() ,
,
解得![]() 或
或![]() ,
,
解得![]() 或
或![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年8月20日起,市交警支队全面启动路口秩序环境综合治理,重点整治机动车不礼让斑马线和行人的行为,经过一段时间的治理,从市交警队数据库中调取了20个路口近三个月的车辆违章数据,经统计得如图所示的频率分布直方图,统计数据中凡违章车次超过30次的设为“重点关注路口”.
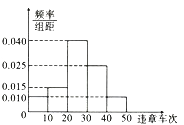
(1)现从“重点关注路口”中随机抽取两个路口安排交警去执勤,求抽出来的路口的违章车次一个在![]() ,一个在
,一个在![]() 中的概率;
中的概率;
(2)现从支队派遣5位交警,每人选择一个路口执勤,每个路口至多1人,违章车次在![]() 的路口必须有交警去,违章车次在
的路口必须有交警去,违章车次在![]() 的不需要交警过去,设去“重点关注路口”的交警人数为
的不需要交警过去,设去“重点关注路口”的交警人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
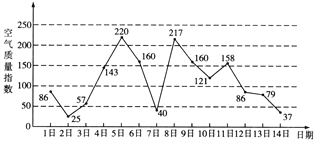
(Ⅰ)求3月1日到14日空气质量指数的中位数;
(Ⅱ)求此人到达当日空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品按行业生产标准分成8个等级,等级系数X依次为1,2,…8,其中![]() 为标准,
为标准,![]() 为标准. 已知甲厂执行标准生产该产品,产品的零售价为6元/件; 乙厂执行标准生产该产品,产品的零售价为元/件,假定甲, 乙两厂的产品都符合相应的执行标准.
为标准. 已知甲厂执行标准生产该产品,产品的零售价为6元/件; 乙厂执行标准生产该产品,产品的零售价为元/件,假定甲, 乙两厂的产品都符合相应的执行标准.
(Ⅰ)已知甲厂产品的等级系数![]() 的概率分布列如下所示:
的概率分布列如下所示:
| 5 | 6 | 7 | 8 |
0.4 | b | 0.1 |
且![]() 的数学期望
的数学期望![]() , 求a,b的值;
, 求a,b的值;
(Ⅱ)为分析乙厂产品的等级系数![]() ,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:

用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数![]() 的数学期望;
的数学期望;
(Ⅲ)在(Ⅰ),(Ⅱ)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注: ①产品的“性价比”=![]() ;②“性价比”大的产品更具可购买性.
;②“性价比”大的产品更具可购买性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com