分析:(Ⅰ)表示出f
n(x),根据零点判定定理可得函数在区间(
,1)内存在零点,利用导数可判断函数单调,从而可得零点的唯一性;
(Ⅱ)对任意的x
1,x
2∈[-1,1],均有|f
2(x
1)-f
2(x
2)丨≤4等价于f
2(x)在[-1,1]上的最大值与最小值之差M=f(x)
max-f(x)
min≤4,按照对称轴在区间[-′1,1]的外边、内部进行分类讨论,可得函数的最大值、最小值及最大值与最小值的差.
解答:解:(Ⅰ)n≥2,b=1,c=-1时,f
n(x)=x
n+x-1,
∵
fn()•f
n(1)=
(-)×1<0,
∴f
n(x)在区间(
,1)内存在零点,
又
f′n(x)=nxn-1+1>0,
∴f
n(x)在区间(
,1)上是单调递增函数,
故f
n(x)在区间(
,1)内存在唯一的零点;
当n=2时,
f2(x)=x2+bx+c,
(Ⅱ)对任意的x
1,x
2∈[-1,1],均有|f
2(x
1)-f
2(x
2)丨≤4等价于f
2(x)在[-1,1]上的最大值与最小值之差M=f(x)
max-f(x)
min≤4,
据此分类讨论如下:
(1)当|
|>1,即|b|>2时,M=|f
2(1)-f
2(-1)|=2|b|>4,与题设矛盾;
(2)当-1
≤-<0,即0<b≤2时,M=
f2(1)-f2(-)=
(+1)2≤4恒成立;
(3)当0<-
≤1,即-2≤b≤0时,M=
f2(-1)-f2(-)=
(-1)2≤4恒成立;
综上知-2≤b≤2.
点评:本题考查函数的零点判定定理、函数恒成立问题,转化为函数最值是解决恒成立问题的常用方法.



 阅读快车系列答案
阅读快车系列答案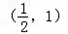 内存在唯一的零点;
内存在唯一的零点;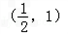 内的零点,判断数列x2,x3,…,xn…的增减性。
内的零点,判断数列x2,x3,…,xn…的增减性。