
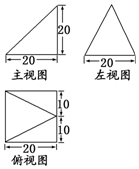
 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.  开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $cos\frac{π}{5}$ | B. | $-cos\frac{π}{5}$ | C. | $±cos\frac{π}{5}$ | D. | $sin\frac{π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “|x|<2”是“x2-x-6<0”的充分不必要条件 | |
| C. | 命题“存在∈R,使得x2+x+1<0”的否定是“对任意x∈R,均有x2+x+1≥0” | |
| D. | 若p∧q为假命题,则p,q均为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
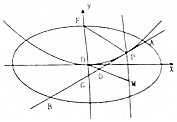 平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
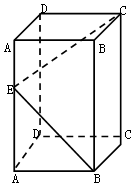 长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )
长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
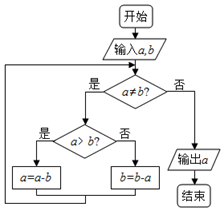 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )| A. | 9 | B. | 3 | C. | 7 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com