
【题目】已知函数f(x)= ![]() ﹣mx(m∈R).
﹣mx(m∈R).
(1)当m=0时,求函数f(x)的零点个数;
(2)当m≥0时,求证:函数f(x)有且只有一个极值点;
(3)当b>a>0时,总有 ![]() >1成立,求实数m的取值范围.
>1成立,求实数m的取值范围.
【答案】
(1)解:m=0时,f(x)= ![]() ,(x>0),f′(x)=
,(x>0),f′(x)= ![]() ,
,
令f′(x)>0,解得:0<x<e,令f′(x)<0,解得:x>e,
∴f(x)在(0,e)递增,在(e,+∞)递减,
∵f(x)max=f(e)= ![]() >0,f(
>0,f( ![]() )=﹣e<0,
)=﹣e<0,
∴f(x)在(0,e)有且只有一个零点,
x>e时,f(x)>0恒成立,
∴f(x)在(e,+∞)无零点,
综上,m=0时,f(x)有且只有一个零点;
(2)证明:∵f(x)= ![]() ﹣mx(m≥0),
﹣mx(m≥0),
f′(x)= ![]() (x>0),
(x>0),
令g(x)=1﹣lnx﹣mx2,g′(x)=﹣ ![]() ﹣2mx<0,
﹣2mx<0,
∴g(x)在(0,+∞)递减,
∵g( ![]() )=1+
)=1+ ![]() ﹣
﹣ ![]() >0,(∵em>m),g(e)=﹣me2<0,
>0,(∵em>m),g(e)=﹣me2<0,
∴x0∈(0,+∞),使得g(x0)=0,
∴x∈(0,x0)时,g(x)>0,f′(x)>0,f(x)在(0,x0)递增,
x∈(x0,+∞)时,g(x)<0,f′(x)<0,f(x)在(0,x0)递减,
∴x=x0是f(x)的极大值点,
即m≥0时,函数f(x)有且只有一个极值点;
(3)解:∵b>a>0时,总有 ![]() >1成立,
>1成立,
即b>a>0时,总有f(b)﹣b>f(a)﹣a成立,
也就是函数h(x)=f(x)﹣x在区间(0,+∞)递增,
由h(x)= ![]() ﹣(m+1)x(x>0)得:h′(x)=
﹣(m+1)x(x>0)得:h′(x)= ![]() ﹣(m+1)≥0在(0,+∞)恒成立,
﹣(m+1)≥0在(0,+∞)恒成立,
即m≤ ![]() ﹣1在(0,+∞)恒成立,
﹣1在(0,+∞)恒成立,
设k(x)= ![]() ﹣1,则k′(x)=
﹣1,则k′(x)= ![]() (x>0),
(x>0),
∴令k′(x)>0,解得:x> ![]() ,令k′(x)<0,解得:0<x<
,令k′(x)<0,解得:0<x< ![]() ,
,
∴k(x)在(0, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴k(x)min=k( ![]() )=﹣
)=﹣ ![]() ﹣1,
﹣1,
故所求m的范围是(﹣,﹣ ![]() ﹣1).
﹣1).
【解析】(1)求出函数的导数,得到函数的单调区间,求出函数的最大值,从而得到函数的零点个数;(2)求出f(x)的导数得到g(x)=1﹣lnx﹣mx2 , 求出g(x)的导数,根据函数的单调性证明函数的零点个数即可;(3)问题转化为函数h(x)=f(x)﹣x在区间(0,+∞)递增,由h(x)= ![]() ﹣(m+1)x(x>0),求出h(x)的导数,根据函数的单调性得到m≤
﹣(m+1)x(x>0),求出h(x)的导数,根据函数的单调性得到m≤ ![]() ﹣1在(0,+∞)恒成立,从而求出m的范围.
﹣1在(0,+∞)恒成立,从而求出m的范围.
【考点精析】本题主要考查了函数的极值与导数和函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图: 
(1)已知男生组中数据的中位数为125,女生组数据的平均数为124,求x,y的值;
(2)现从这20名学生中任意抽取一名男生和一名女生对他们进行训练,记一分钟内跳绳次数不低于115且不超过125的学生被选上的人数为X,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=
的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=![]() AB=1,点M在线段EC上.
AB=1,点M在线段EC上.
(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥O﹣ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.

(1)求异面直线BE与AC所成角的余弦值;
(2)求直线BE和平面ABC的所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
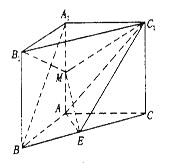
(Ⅰ)求证:A1B//平面AEC1;
(Ⅱ)在棱AA1上存在一点M,满足![]() ,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两名工人加工同一种零件,两人每天加工的零件数相同,所得次品数分别为![]() ,
,![]() ,
,![]() 和
和![]() 的分布列如下表.
的分布列如下表.

(![]() )分别求期望
)分别求期望![]() 和
和![]() .
.
(![]() )试对这两名工人的技术水平进行比较.
)试对这两名工人的技术水平进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.
(2)根据以上数据完成如下2×2列联表.

(3)能否有99%的把握认为其亲属的饮食习惯与年龄有关?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,对于给定的
时,对于给定的![]() ,且
,且![]() ,
,![]() ,证明:关于
,证明:关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有一个实根.
内有一个实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com