
【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
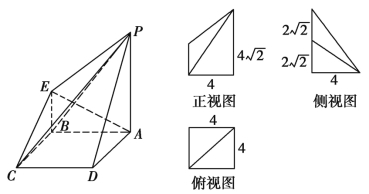
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为![]() .
.
(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
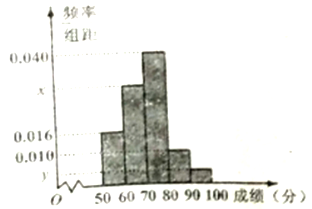

(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
, ![]() 的值;
的值;
(Ⅱ)分数在![]() 的学生设为一等奖,获奖学金500元;分数在
的学生设为一等奖,获奖学金500元;分数在![]() 的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数
,求非零常数![]() 的值.
的值.
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在正整数
项和,是否存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=![]() , AD=1,DC⊥BC,则这块菜地的面积为
, AD=1,DC⊥BC,则这块菜地的面积为 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在(﹣∞,0)上单调递减,且f(2)=0,则不等式xf(x﹣1)>0的解集是( )
A.(﹣3,﹣1)
B.(﹣3,1)∪(2,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣1,0)∪(1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com