
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() 、
、![]() ,并且经过点
,并且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() :
:![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() .当
.当![]() ,且满足
,且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
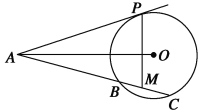
(1)证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为3的正三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,满足
边上的点,满足![]() (如图
(如图![]() ),将
),将![]() 折起到
折起到![]() 的位置上,连接
的位置上,连接![]() (如图).
(如图).
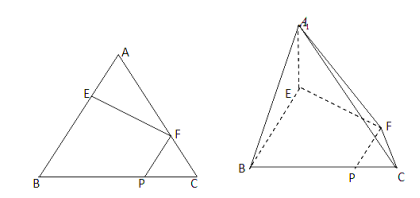
(1)在线段A1C上是否存在点Q,使得面QFP//面A1EB,证明你的结论;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
④“平面向量![]() 与
与![]() 的夹角是钝角”的要条件是“
的夹角是钝角”的要条件是“![]() ”.
”.
其中正确命题的序号是 .(把所有正确命题的序号都写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
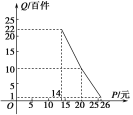
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016 年1 月1 日起全国统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取![]() 后和
后和![]() 后作为调查对象,随机调查了
后作为调查对象,随机调查了![]() 位,得到数据如下表:
位,得到数据如下表:
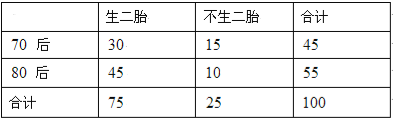
(Ⅰ)以这![]() 个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市
个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市![]() 后公民中随机抽取
后公民中随机抽取![]() 位,记其中生二胎的人数为
位,记其中生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据调查数据,是否有 ![]() 以上的把握认为“生二胎与年龄有关”,并说明理由:
以上的把握认为“生二胎与年龄有关”,并说明理由:
参考数据:

(参考公式: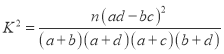 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com