
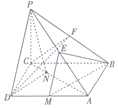
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.分析 (1)推导出DC⊥PC,DC⊥BC,从而DC⊥PB,再求出CF⊥PB,由此能证明PB⊥平面CDF.
(2)过点D作交BC于G,连接PG,当N是AC与DG的交点时,平面PDN∥平面BEM,由此能求出当$\frac{CN}{AC}$=$\frac{1}{3}$时,平面PDN∥平面BEM.
解答 证明:(1)∵PC⊥底面ABCD,底面ABCD是矩形,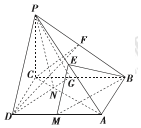
∴DC⊥PC,DC⊥BC,又PC∩BC=C,∴DC⊥平面PBC,…(2分)
∴DC⊥PB.…(4分)
∵BC=PC,F为PB的中点,∴CF⊥PB.…(5分)
∵DC∩CF=C,∴PB⊥平面CDF.…(6分)
解:(2)过点D作交BC于G,连接PG,…(7分)
∵M是AD的中点,∴EM∥PD,…(8分)
∵PD∩DG=D,∴平面PDG∥平面BEM,…(9分)
∴当N是AC与DG的交点时,平面PDN∥平面BEM,…(10分)
∴在矩形ABCD中,由题意得$\frac{CN}{AC}=\frac{1}{3}$.
故当$\frac{CN}{AC}$=$\frac{1}{3}$时,平面PDN∥平面BEM.…(12分)
点评 本题考查线面垂直的证明,考查满足面面平行的点的位置的判断与求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | m∥n,n∥α⇒m∥α | B. | α⊥β,α∩β=m,l⊥m⇒l⊥β | ||
| C. | l⊥m,l⊥n,m?α,n?α⇒l⊥α | D. | m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.
已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{\sqrt{3}}}{6}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a-1 | B. | 2-a-1 | C. | 1-2-a | D. | 1-2a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com