
 已知函数f(x)=2sin(ωx+φ)(ω>0,-
已知函数f(x)=2sin(ωx+φ)(ω>0,-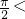 φ<
φ< )的图象如图所示,直线x=
)的图象如图所示,直线x= ,x=
,x= 是其两条对称轴.
是其两条对称轴. ,且
,且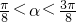 ,求f(
,求f(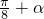 )的值.
)的值. =
= -
- =
= ,∴T=π.
,∴T=π. )=2sin(
)=2sin( +φ)=2,解得φ=2kπ-
+φ)=2,解得φ=2kπ- (k∈Z).
(k∈Z). <φ<
<φ< ,∴φ=-
,∴φ=- ,∴f(x)=2sin(2x-
,∴f(x)=2sin(2x- ).(5分)
).(5分) ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z),知kπ-
(k∈Z),知kπ- ≤x≤kπ+
≤x≤kπ+ (k∈Z),
(k∈Z), ,kπ+
,kπ+ ](k∈Z).(7分)
](k∈Z).(7分) )=
)= ,即sin(2α-
,即sin(2α- )=
)= ,(8分)
,(8分) <α<
<α< ,∴0<2α-
,∴0<2α- <
< .
. )=
)= ,(10分)
,(10分) +α)=2sin[(2α-
+α)=2sin[(2α- )+
)+ ].
]. )+
)+ ]=sin(2α-
]=sin(2α- )cos
)cos +cos(2α-
+cos(2α- )sin
)sin =
= (
( +
+ )=
)= ,
, +α)=
+α)=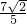 .(14分)
.(14分) )=
)= ,得sin2α-cos2α=
,得sin2α-cos2α=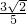 ,①(9分)
,①(9分) <α<
<α< ,∴0<2α-
,∴0<2α- <
< ,
, )=
)= ,(11分)
,(11分) )=
)= 得sin2α+cos2α=
得sin2α+cos2α= .②
.②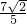 ,
, +α)=
+α)=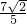 .(14分)
.(14分) ,求出sin(2α-
,求出sin(2α- )=
)= ,利用f(
,利用f( +α)=2sin[(2α-
+α)=2sin[(2α- )+
)+ ]然后求出值.
]然后求出值. ,求出cos(2α-
,求出cos(2α- )=
)= ,求出sin2α,然后利用f(
,求出sin2α,然后利用f( +α)=2sin[(2α-
+α)=2sin[(2α- )+
)+ ]
]

 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com