
【题目】如图,某学校拟建一块五边形区域的“读书角”,三角形区域ABE为书籍摆放区,沿着AB、AE处摆放折线形书架(书架宽度不计),四边形区域为BCDE为阅读区,若∠BAE=60°,∠BCD=∠CDE=120°,DE=3BC=3CD=![]() m.
m.
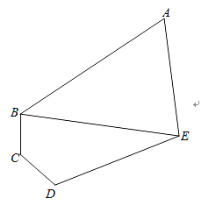
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求书架总长度AB+AE的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)连接BD,由余弦定理可得BD,由已知可求∠CDB=∠CBD=30°,∠CDE=120°,可得∠BDE=90°,利用勾股定理即可得解BE的值;(2)设∠ABE=α,由正弦定理,可得AB=4![]() sin(120°﹣α),AE=4
sin(120°﹣α),AE=4![]() sinα,利用三角函数恒等变换的应用化简可得AB+AE=12sin(α+30°),结合范围60°<α+30°<120°,利用正弦函数的性质可求AB+AE的最大值,从而得解.
sinα,利用三角函数恒等变换的应用化简可得AB+AE=12sin(α+30°),结合范围60°<α+30°<120°,利用正弦函数的性质可求AB+AE的最大值,从而得解.
⑴连接BD,在△BDC中,![]() ,∠BCD=120°,
,∠BCD=120°,
由余弦定理![]() ,
,
得![]() ,得
,得![]()
又BC=CD,∠BCD=120°,
![]() ,
,![]() .
.
△ABE中,BD=3,![]() ,由勾股定理
,由勾股定理![]() .
.
故![]() .
.
⑵设![]() ,
,
则![]() ,
,
在△ABE中,
由正弦定理![]() .
.
![]() ,
,![]() ,
,
故![]()
=![]()
![]() ,
,
△ABE为锐角三角形,
故![]() ,
,![]() ,
,
![]() ,
,![]()
所以暑假的总长度AB+AE的取值范围是![]() ,
,


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (限定
(限定![]() ).
).
(1)写出曲线![]() 的极坐标方程,并求
的极坐标方程,并求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)射线![]() 与曲线
与曲线![]() 与
与![]() 分别交于点
分别交于点![]() (
(![]() 异于原点),求
异于原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在边长为4的正方形ABCD中,E,F分别是边AB,BC上的点(端点除外),将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′(如图②).
(1)求证:A′D⊥EF;
(2)当点E,F分别为AB,BC的中点时,求直线A′E与直线BD所成角的余弦值.
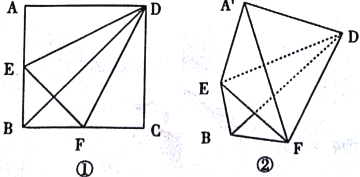
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为左,右焦点,
分别为左,右焦点,![]() 分别为左,右顶点,D为上顶点,原点
分别为左,右顶点,D为上顶点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设点
.设点![]() 在第一象限,纵坐标为t,且
在第一象限,纵坐标为t,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() .
.
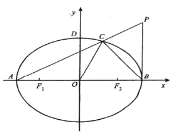
(1)求椭圆![]() 的方程;
的方程;
(2)(文)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求直线
的面积,求直线![]() 的方程;
的方程;
(理)求过点![]() 的圆方程(结果用t表示)
的圆方程(结果用t表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知椭圆两个焦点的坐标分别是(-2,0),(2,0),并且经过点![]() ,求它的标准方程;
,求它的标准方程;
(2)已知双曲线两个焦点的坐标分别是(0,-6),(0,6),并且经过点(2,-5),求它的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均为正数且公比不等于1的等比数列
是各项均为正数且公比不等于1的等比数列![]() ,对于函数
,对于函数![]() ,若数列
,若数列![]() 为等差数列,则称函数
为等差数列,则称函数![]() 为“保比差数列函数”,现有定义在
为“保比差数列函数”,现有定义在![]() 上的如下函数:①
上的如下函数:①![]() ,②
,②![]() ,③
,③![]() ;④
;④![]() ,则为“保比差数列函数”的所有序号为( )
,则为“保比差数列函数”的所有序号为( )
A.①②B.①②④C.③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com