
已知复数z=bi(b∈R),![]() 是实数,i是虚数单位.
是实数,i是虚数单位.
(1)求复数z;
(2)若复数(m+z)2所表示的点在第一象限,求实数m的取值范围.
考点:
复数代数形式的混合运算;复数的基本概念.
专题:
计算题.
分析:
(1)由z=bi(b∈R),化简![]() 为
为![]() .根据
.根据![]() 是实数,可得
是实数,可得![]() ,求得 b的值,可得z的值.
,求得 b的值,可得z的值.
(2)化简 (m+z)2为 (m2﹣4)﹣4mi,根据复数f(4)所表示的点在第一象限,可得![]() ,解不等式组求得实数m的取值范围.
,解不等式组求得实数m的取值范围.
解答:
解:(1)∵z=bi(b∈R),∴![]() =
=![]() =
=![]() =
=![]() .
.
又∵![]() 是实数,∴
是实数,∴![]() ,
,
∴b=﹣2,即z=﹣2i.
(2)∵z=﹣2i,m∈R,∴(m+z)2=(m﹣2i)2=m2﹣4mi+4i2=(m2﹣4)﹣4mi,
又∵复数f(4)所表示的点在第一象限,∴![]() ,…(10分)
,…(10分)
解得m<﹣2,即m∈(﹣∞,﹣2)时,复数f(4)所表示的点在第一象限.
点评:
本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,虚数单位i的幂运算性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
| z-2 |
| 1+i |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省东莞市高二(下)期末数学试卷A(理科)(解析版) 题型:解答题
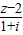 是实数,i是虚数单位.
是实数,i是虚数单位.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com