
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直,求
轴垂直,求![]() 的值;
的值;
(2)若![]() ,试探究函数
,试探究函数![]() 与
与![]() 的图象在其公共点处是否存在公切线.若存在,研究
的图象在其公共点处是否存在公切线.若存在,研究![]() 值的个数;,若不存在,请说明理由.
值的个数;,若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处不存在公切线,当
的图象在其公共点处不存在公切线,当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处存在公切线,且符合题意的
的图象在其公共点处存在公切线,且符合题意的![]() 的值有且仅有两个.
的值有且仅有两个.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,得到
,得到![]() ,依题意
,依题意![]() ,即可求解
,即可求解![]() 的值;(2)假设
的值;(2)假设![]() 的图象在其公共点
的图象在其公共点![]() 处存在公切线,分别求出导数,令
处存在公切线,分别求出导数,令![]() ,得
,得![]() ,讨论
,讨论![]() ,分别
,分别![]() ,
, ![]() ,令
,令![]() ,研究方程解的个数,可构造函数,运用都是求出单调区间,讨论函数的零点个数即可判断.
,研究方程解的个数,可构造函数,运用都是求出单调区间,讨论函数的零点个数即可判断.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
依题意得![]() ,∴
,∴ ![]() .
.
(2)假设函数![]() 与
与![]() 的图象在其公共点
的图象在其公共点![]() 处存在公切线,
处存在公切线,
∵![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
由![]() 得
得![]() ,即
,即![]() ,
,
∴![]() ,故
,故![]() .
.
∵函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时, ![]() ,∴函数
,∴函数![]() 与
与![]() 的图象在其公共点处不存在公切线;
的图象在其公共点处不存在公切线;
当![]() 时,令
时,令![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() (
(![]() ).
).
下面研究满足此等式的![]() 的值的个数:
的值的个数:
设![]() ,则
,则![]() ,且
,且![]() ,方程
,方程![]() 化为
化为![]() ,
,
分别画出![]() 和
和![]() 的图象,
的图象,
当![]() 时,
时, ![]() ,
, ![]() ,
,
由函数图象的性质可得![]() 和
和![]() 的图象有且只有两个公共点(且均符合),
的图象有且只有两个公共点(且均符合),
∴方程![]() 有且只有两个根.
有且只有两个根.
综上,当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处不存在公切线;当
的图象在其公共点处不存在公切线;当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处存在公切线,且符合题意的
的图象在其公共点处存在公切线,且符合题意的![]() 的值有且仅有两个.
的值有且仅有两个.
点晴:本题主要考查了导数在函数中的综合应用问题,其中解答中涉及到了利用导数求解曲线在某点处的切线方程,利用导数研究函数的单调性,利用函数的性质解决不等式、方程问题,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,本题的解答中认真审题,注意导数在函数中的合理应用,试题有一定的难度,属于难题.


科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)=-f(x)且f(x)在[-1,0]上是增函数,给出下列四个命题:
①f(x)是周期函数;②f(x)的图象关于x=1对称;③f(x)在[1,2]上是减函数;④f(2)=f(0).
其中正确命题的序号是____________.(请把正确命题的序号全部写出来)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图与侧视图是腰长为6的等腰直角三角形,俯视图是正方形.
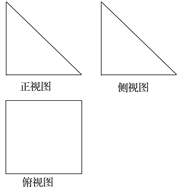
(1)请画出该几何体的直观图,并求出它的体积;
(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1?如何组拼?试证明你的结论;
(3)在(2)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
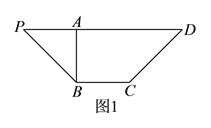
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
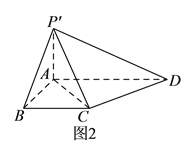
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1:乙套设备的样本的频率分布直方图

(1)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ,求 |
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
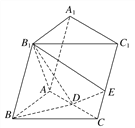
【题目】如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
(1)求证:平面ABB1A1⊥平面ABC;
(2)在线段CC1(不含端点)上,是否存在点E,使得二面角E-B1D-B的余弦值为-![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com