[题目]下列函数在其定义域中.既是奇函数又是增函数的( )A.y=x+1B.y=﹣x2C.y=x|x|D. 题目和参考答案——青夏教育精英家教网—

【题目】下列函数在其定义域中，既是奇函数又是增函数的（）
A.y=x+1
B.y=﹣x2
C.y=x|x|
D.

【答案】C
【解析】解：因y=x+1的图象不关于原点对称，所以不是奇函数，不符合题意；
y=﹣x2在定义域R上为偶函数，不符合题意；
因函数y=x|x|的定义域为R，且（﹣x）|﹣x|=﹣x|x|，所以为奇函数，
又y=x|x|= ，则函数y=x|x|在[0，+∞），（﹣∞，0）上单调递增，
∵02=﹣02 ， ∴该函数在定义域R上是增函数，符合题意；
由于函数y=﹣ 是奇函数，但在定义域（﹣∞，0）∪（0，+∞）上不是增函数，不符合题意．
故选C．
利用函数奇偶性的定义判断各个选项中的函数的奇偶性，化简后由基本初等函数的单调性，判断函数在定义域上的单调性，从而得出答案．

练习册系列答案

名校秘题小学毕业升学系统总复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】一生物科研小组对升高温度的多少与某种细菌种群存活数量之间的关系进行分析研究，他们制作5 份相同的样本并编号1、2、3、4、5，分别记录它们同在下升高不同的温度后的种群存活数量，得到如下资料：

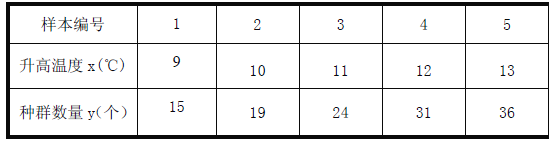
（1）若随机选取2份样本的数据来研究，求其编号不相邻的概率；

（2）求出关于的线性回归方程；

（3）利用（2）中所求出的回归方程预测温度升高15 时此种样本中种菌群存活数量.

附：，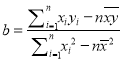

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定点M（﹣ ），N是圆C：（x﹣ ）2+y2=16（C为圆心）上的动点，MN的垂直平分线与NC交于点E．
（1）求动点E的轨迹方程C1；
（2）直线l与轨迹C1交于P，Q两点，与抛物线C2：x2=4y交于A，B两点，且抛物线C2在点A，B处的切线垂直相交于S，设点S到直线l的距离为d，试问：是否存在直线l，使得d= ？若存在，求直线l的方程；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】电视传媒公司为了解某地区电视观众对里约奥运会的收视情况，随机抽取了100名观众进行调查，其中女性有55名，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：

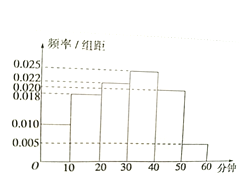
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”。已知“体育迷”中有10名女性。

（1）试求“体育迷”中的男性观众人数；

（2）据此资料完成列联表，你是否认为“体育迷”与性别有关？

	非体育迷	体育迷	合计
男
女
合计

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

临界值表供参考参考公式：

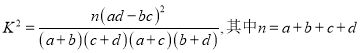
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：
（i）对任意的x∈[0，1]，恒有f（x）≥0；
（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．
则下列四个函数中不是M函数的个数是（）
①f（x）=x2②f（x）=x2+1
③f（x）=ln（x2+1）④f（x）=2x﹣1．
A.1
B.2
C.3
D.4