
【题目】如图,三棱台![]() 中, 侧面
中, 侧面![]() 与侧面
与侧面![]() 是全等的梯形,若
是全等的梯形,若![]() ,且
,且![]() .
.

(Ⅰ)若![]() ,
, ![]() ,证明:
,证明: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若二面角![]() 为
为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是
甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
由此判断性能较好的一台是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2﹣2ax+b2=0.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“正多边形都相似”的逆命题;
③“若m>0,则x2+x﹣m=0有实根”的逆否命题;
④“若x﹣ ![]() 是有理数,则x是无理数”的逆否命题.
是有理数,则x是无理数”的逆否命题.
A.①②③④
B.①③④
C.②③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学在五次考试中数学成绩统计用茎叶图如表示如图2所示,则甲的平均成绩比乙的平均成绩(填高、低、相等);甲成绩的方差比乙成绩的方差(填大、小) 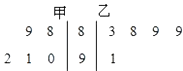
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的叙述,错误的个数为( )
①若p∨q为真命题,则p∧q为真命题
②“x>5”是“x2﹣4x﹣5>0”的充分不必要条件
③命题p:x∈R,使得x2+x﹣1<0,则¬p:x∈R,使得x2+x﹣1≥0
④命题“若x2﹣3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2﹣3x+2≠0”
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O的方程为x2+y2=5.
(1)P是直线y= ![]() x﹣5上的动点,过P作圆O的两条切线PC、PD,切点为C、D,求证:直线CD过定点;
x﹣5上的动点,过P作圆O的两条切线PC、PD,切点为C、D,求证:直线CD过定点;
(2)若EF、GH为圆O的两条互相垂直的弦,垂足为M(1,1),求四边形EGFH面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com