
【题目】已知函数f(x)=2sin(ωx),其中常数ω>0
(1)令ω=1,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)令ω=2,将函数y=f(x)的图象向左平移个![]() 单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
【答案】(1)F(x)既不是奇函数,也不是偶函数(2)21或20
【解析】
(1)特值法:ω=1时,写出f(x)、F(x),求出F(![]() )、F(
)、F(![]() ),结合函数奇偶性的定义可作出正确判断;
),结合函数奇偶性的定义可作出正确判断;
(2)根据图象平移变换求出g(x),令g(x)=0可得g(x)可能的零点,而[a,a+10π]恰含10个周期,分a是零点,a不是零点两种情况讨论,结合图象可得g(x)在[a,a+10π]上零点个数的所有可能值.
(1)f(x)=2sinx,
F(x)=f(x)+f(x![]() )=2sinx+2sin(x
)=2sinx+2sin(x![]() )=2(sinx+cosx),
)=2(sinx+cosx),
F(![]() )=2
)=2![]() ,F(
,F(![]() )=0,F(
)=0,F(![]() )≠F(
)≠F(![]() ),F(
),F(![]() )≠﹣F(
)≠﹣F(![]() ),
),
所以,F(x)既不是奇函数,也不是偶函数.
(2)f(x)=2sin2x,
将y=f(x)的图象向左平移![]() 个单位,再向上平移1个单位后得到y=2sin2(x
个单位,再向上平移1个单位后得到y=2sin2(x![]() )+1的图象,所以g(x)=2sin2(x
)+1的图象,所以g(x)=2sin2(x![]() )+1.
)+1.
令g(x)=0,得x=kπ![]() 或x=kπ
或x=kπ![]() (k∈z),
(k∈z),
因为[a,a+10π]恰含10个周期,所以,当a是零点时,在[a,a+10π]上零点个数21,
当a不是零点时,a+kπ(k∈z)也都不是零点,区间[a+kπ,a+(k+1)π]上恰有两个零点,故在[a,a+10π]上有20个零点.
综上,y=g(x)在[a,a+10π]上零点个数的所有可能值为21或20.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 与直线
与直线![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.

(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,点M是PQ的中点,直线
两点,点M是PQ的中点,直线![]() 与直线
与直线![]() 相交于点N.探索
相交于点N.探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小威初三参加某高中学校的数学自主招生考试,这次考试由十道选择题组成,得分要求是:做对一道题得1分,做错一道题扣去1分,不做得0分,总得分7分就算及格,小威的目标是至少得7分获得及格,在这次考试中,小威确定他做的前六题全对,记6分,而他做余下的四道题中,每道题做对的概率均为p![]() ,考试中,小威思量:从余下的四道题中再做一题并且及格的概率
,考试中,小威思量:从余下的四道题中再做一题并且及格的概率![]() ;从余下的四道题中恰做两道并且及格的概率
;从余下的四道题中恰做两道并且及格的概率![]() ,他发现
,他发现![]() ,只做一道更容易及格.
,只做一道更容易及格.
(1)设小威从余下的四道题中恰做三道并且及格的概率为![]() ,从余下的四道题中全做并且及格的概率为
,从余下的四道题中全做并且及格的概率为![]() ,求
,求![]() 及
及![]() ;
;
(2)由于p的大小影响,请你帮小威讨论:小威从余下的四道题中恰做几道并且及格的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
(1)求证:AE∥平面BDF;
(2)求证:平面BDF⊥平面ACE;
(3)2AE=EB,在线段AE上找一点P,使得二面角P﹣DB﹣F的余弦值为![]() , 求AP的长.
, 求AP的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sin(2x﹣![]() )的图象向左平移
)的图象向左平移![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,则b的最小值为
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,则b的最小值为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名男生、3名女生站成一排:
(1)女生都不站在两端,有多少不同的站法?
(2)三名男生要相邻,有多少种不同的站法?
(3)三名女生互不相邻,三名男生也互不相邻,有多少种不同的站法?
(4)女生甲,女生乙都不与男生丙相邻,有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了调查某市同时符合条件![]() 与
与![]() (条件
(条件![]() :营养均衡,作息规律;条件
:营养均衡,作息规律;条件![]() :经常锻炼,劳逸结合)的高中男生的体重
:经常锻炼,劳逸结合)的高中男生的体重![]() (单位:
(单位:![]() )与身高
)与身高![]() (单位:
(单位: ![]() )是否存在较好的线性关系,该机构搜集了
)是否存在较好的线性关系,该机构搜集了![]() 位满足条件的高中男生的数据,得到如下表格:
位满足条件的高中男生的数据,得到如下表格:
身高/ |
|
|
|
|
|
|
体重/ |
|
|
|
|
|
|
根据表中数据计算得到![]() 关于
关于![]() 的线性回归方程对应的直线的斜率为
的线性回归方程对应的直线的斜率为![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到整数部分);
精确到整数部分);
(2)已知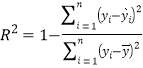 ,且当
,且当![]() 时,回归方程的拟合效果较好。试结合数据
时,回归方程的拟合效果较好。试结合数据![]() ,判断(1)中的回归方程的拟合效果是否良好?
,判断(1)中的回归方程的拟合效果是否良好?
(3)该市某高中有![]() 位男生同时符合条件
位男生同时符合条件![]() 与
与![]() ,将这
,将这![]() 位男生的身高(单位:
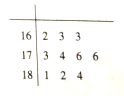
位男生的身高(单位:![]() )的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这
)的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这![]() 位男生的体重未超过
位男生的体重未超过![]() 的所有男生体重(单位:
的所有男生体重(单位:![]() )的平均数(结果精确到整数部分).
)的平均数(结果精确到整数部分).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 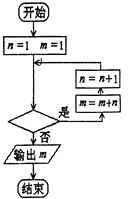
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某居民小区有两个相互独立的安全防范系统(简称系统)![]() 和
和![]() ,系统
,系统![]() 和
和![]() 在任意时刻发生故障的概率分别为
在任意时刻发生故障的概率分别为![]() 和
和![]() 。
。
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)设系统![]() 在3次相互独立的检测中不发生故障的次数为随机变量
在3次相互独立的检测中不发生故障的次数为随机变量![]() ,求
,求![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com