
【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1= ![]() 且13a2=3S3(n∈N*).
且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=nan , 求数列{bn}的前项n和Tn .
【答案】
(1)解:设等比数列{an}的公比为q<1,∵a1= ![]() ,且13a2=3S3(n∈N*).
,且13a2=3S3(n∈N*).
∴13a1q=3a1(1+q+q2),化为:3q2﹣10q+3=0,q<1,解得q= ![]() .
.
∴an= ![]() =2×
=2× ![]()
(2)解:bn=nan= ![]() .
.
∴数列{bn}的前项n和Tn= ![]() +…+
+…+ ![]() ,
,
∴ ![]() =2
=2 ![]() +…+(n﹣1)×
+…+(n﹣1)× ![]() +n×
+n× ![]() ,
,
∴ ![]() =2
=2 ![]() =2
=2 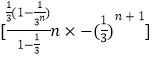 =1﹣
=1﹣ ![]() ,
,
∴Tn= ![]() ﹣
﹣ ![]()
【解析】(1)设等比数列{an}的公比为q<1,根据a1= ![]() ,且13a2=3S3(n∈N*).可得13a1q=3a1(1+q+q2),解出即可得出.(2)bn=nan=
,且13a2=3S3(n∈N*).可得13a1q=3a1(1+q+q2),解出即可得出.(2)bn=nan= ![]() .利用“错位相减法”与等比数列的前项n和公式即可得出.
.利用“错位相减法”与等比数列的前项n和公式即可得出.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系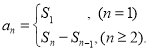 ).
).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax-1(x≥0).其中a>0,a≠1.
(1)若f(x)的图象经过点(![]() ,2),求a的值;
,2),求a的值;
(2)求函数y=f(x)(x≥0)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中φ∈(0, ![]() ),则函数g(x)=cos(2x﹣φ)的图象( )
),则函数g(x)=cos(2x﹣φ)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.可由函数f(x)的图象向右平移 ![]() 个单位得到
个单位得到
C.可由函数f(x)的图象向左平移 ![]() 个单位得到
个单位得到
D.可由函数f(x)的图象向左平移 ![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若点![]() 为
为![]() 上一点且
上一点且![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= ![]() .
. 
(1)求证:PA⊥BD;
(2)若PC=BC,求二面角A﹣BP﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某专营店经销某商品,当售价不高于10元时,每天能销售100件,当价格高于10元时,每提高1元,销量减少3件,若该专营店每日费用支出为500元,用x表示该商品定价,y表示该专营店一天的净收入(除去每日的费用支出后的收入).
(1)把y表示成x的函数;
(2)试确定该商品定价为多少元时,一天的净收入最高?并求出净收入的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x∈R|x2-3x+b=0},Q={x∈R|(x+1)(x2+3x-4)=0}.
(1)若b=4,存在集合M使得P![]() M
M![]() Q;
Q;
(2)若PQ,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com