
【题目】已知函数![]()
![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若对任意的![]() ,存在
,存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ;
;![]() ,单调递增区间是
,单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;
;![]() ,单调递增区间是
,单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]()
【解析】
(1)先求定义域,再求导,对参数进行分类讨论,研究函数单调性,找出单调区间;
(2)利用(1)中结论,将目标问题转化为最值问题,分离参数,求解即可.
(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
若![]() ,
,![]() .
.
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
若![]() ,令
,令![]() ,
,
解得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 |
![]() 函数
函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;
;
当![]() 时,
时,![]() ,
,![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 |
![]() 函数
函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
综上所述:![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ;
;![]() ,单调递增区间是
,单调递增区间是![]() ,
,
单调递减区间是![]() ;
;![]() ,单调递增区间是
,单调递增区间是![]() ,单调递减区间是
,单调递减区间是
![]()
(2)由(1)可知,函数![]() 在
在![]() 上是单调递增的,
上是单调递增的,
所以![]() ,
,
则![]() 在
在![]() 上恒成立.
上恒成立.
即![]() 在
在![]() 上恒成立.
上恒成立.
因为函数![]() 在
在![]() 是单调递减的,
是单调递减的,
所以,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】从分别写有数字1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数字不大于第二张卡片的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从6名男医生和3名女医生中选出5人组成一个医疗小组,请解答下列问题:
(1)如果这个医疗小组中男女医生都不能少于2人,共有多少种不同的建组方案?(用数字作答)
(2)男医生甲要担任医疗小组组长,所以必选,而且医疗小组必须男女医生都有,共有多少种不同的建组方案?
(3)男医生甲与女医生乙不被同时选中的概率.(化成最简分数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
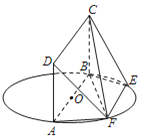
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)当AD=1时,求直线FB与平面DFC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛决赛的500名同学编号为:001,002,...,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽到的号码为005,这500名学生分别在三个考点考试,从001到200在第一考点,从201到365在第二考点,从366到500在第三考点,则第二考点被抽中的人数为( )
A. 15B. 16C. 17D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜批发商分别在甲、乙两市场销售某种蔬菜(两个市场的销售互不影响),己知该蔬菜每售出1吨获利500元,未售出的蔬菜低价处理,每吨亏损100 元.现统计甲、乙两市场以往100个销售周期该蔬菜的市场需求量的频数分布,如下表:
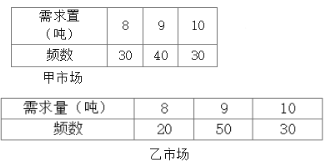
以市场需求量的频率代替需求量的概率.设批发商在下个销售周期购进![]() 吨该蔬菜,在 甲、乙两市场同时销售,以
吨该蔬菜,在 甲、乙两市场同时销售,以![]() (单位:吨)表示下个销售周期两市场的需求量,
(单位:吨)表示下个销售周期两市场的需求量,![]() (单位:元)表示下个销售周期两市场的销售总利润.
(单位:元)表示下个销售周期两市场的销售总利润.
(Ⅰ)当![]() 时,求
时,求![]() 与
与![]() 的函数解析式,并估计销售利润不少于8900元的槪率;
的函数解析式,并估计销售利润不少于8900元的槪率;
(Ⅱ)以销售利润的期望为决策依据,判断![]() 与
与![]() 应选用哪—个.
应选用哪—个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
男 | 女 | 总计 | |
满意 | 50 | 30 | 80 |
不满意 | 10 | 20 | 30 |
总计 | 60 | 50 | 110 |
(1)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关
注:![]()
临界值表:
P( | 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com