
【题目】某校高一新生共有320人,其中男生192人,女生128人.为了解高一新生对数学选修课程的看法,采用分层抽样的方法从高一新生中抽取5人进行访谈.
(Ⅰ)这5人中男生、女生各多少名?
(Ⅱ)从这5人中随即抽取2人完成访谈问卷,求2人中恰有1名女生的概率.
【答案】(Ⅰ)男生3人,女生2人;(Ⅱ)![]()
【解析】
(Ⅰ)利用分层抽样按比例计算出这5人中男生人数和女生人数.
(Ⅱ)记这5人中的3名男生为B1,B2,B3,2名女生为G1,G2,利用列举法能求出抽取的2人中恰有1名女生的概率.
(Ⅰ)这5人中男生人数为![]() ,女生人数为
,女生人数为![]() .
.
(Ⅱ)记这5人中的3名男生为B1,B2,B3,2名女生为G1,G2,
则样本空间为:
Ω={ (B1,B2), (B1,B3), (B1,G1), (B1,G2), (B2,B3), (B2,G1), (B2,G2), (B3,G1), (B3,G2), (G1,G2)},
样本空间中,共包含10个样本点.
设事件A为“抽取的2人中恰有1名女生”,
则A={ (B1,G1), (B1,G2), (B2,G1), (B2,G2), (B3,G1), (B3,G2)},
事件A共包含6个样本点. 从而![]()
所以抽取的2人中恰有1名女生的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]()
![]() (
(![]() )的半焦距为
)的半焦距为![]() ,原点
,原点![]() 到经过两点
到经过两点![]() ,
,![]() 的直线的距离为
的直线的距离为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)如图,![]() 是圆
是圆![]()
![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的![]() 监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).

(1)求这18个数据中不超标数据的平均数与方差;
(2)在空气质量为一级的数据中,随机抽取2个数据,求其中恰有一个为![]() 日均值小于30微克/立方米的数据的概率;
日均值小于30微克/立方米的数据的概率;
(3)以这![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中约有多少天的空气质量超标.
天计算)中约有多少天的空气质量超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的成绩记录,甲、乙两名队员射击中靶环数(环数为整数)的频率分布情况如图所示.假设每名队员每次射击相互独立.

(Ⅰ)求图中a的值;
(Ⅱ)队员甲进行2次射击.用频率估计概率,求甲恰有1次中靶环数大于7的概率;
(Ⅲ)在队员甲、乙中,哪一名队员的射击成绩更稳定?(结论无需证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
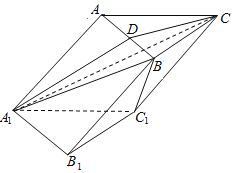
【题目】如图,在底边为等边三角形的斜三棱柱ABC﹣A1B1C1中,AA1![]() AB,四边形B1C1CB为矩形,过A1C作与直线BC1平行的平面A1CD交AB于点D.
AB,四边形B1C1CB为矩形,过A1C作与直线BC1平行的平面A1CD交AB于点D.
(Ⅰ)证明:CD⊥AB;
(Ⅱ)若AA1与底面A1B1C1所成角为60°,求二面角B﹣A1C﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示:
的部分图象如图所示:
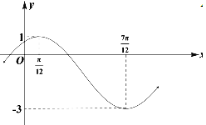
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调区间和对称中心坐标;
的单调区间和对称中心坐标;
(3)将![]() 的图象向左平移
的图象向左平移![]() 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
停车距离 |
|
|
|
|
|
频数 | 24 | 42 | 24 | 9 | 1 |
表2
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
回答以下问题.
(1)由表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(1)中无酒状态下的停车距离平均数的
大于(1)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
(附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为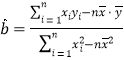 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com